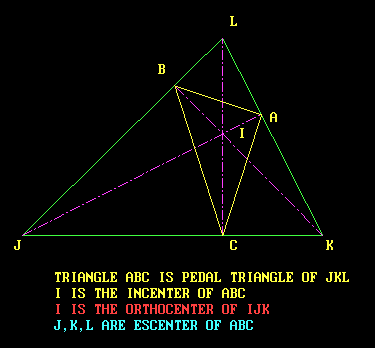
Highlight
- Defintion : See triangle IJK in Figure
- Proof : See MD2002 program 13 03
Q1.
Study Subjects
Five centers of triangle
Questions
- What is ex-center of triangle ?
- What is in-center of triangle ?
- What is es-center of triangle ?
- What is gravity center of triangle ?
- What is orthocenter of triangle ?
Q2. What is ex-central triangle ?
Construction
- Draw triangle ABC
- Draw es-centers J on bisector of angle A of triangle ABC.
- Draw es-centers K on bisector of angle B of triangle ABC.
- Draw es-centers L on bisector of angle C of triangle ABC.
Questions
- 1. Prove that J, C, K are colinear.
- 2. Prove that K, A, L are colinear.
- 3. Prove that L, B, J are colinear.
- 4. Prove that I is the incenter of triangle ABC.
- 5. Prove that I is also the orthocenter of triangle JKL.
Proof
- Prove that K, A, L are colinear.
- Poduce CA to P.
- AL is bisector of angle PAB.
- Angle PAB = (angle B) + (angle C).
- Hence angle LAB = (angle PAB)/2 = (B + C)/2.
- Angle CAJ = (angle A)/2.
- Hence angle LAJ = (angle LAB) + (angle CAJ) = (A + B + C)/2 = 90 degrees.
- Similarly, angle KAJ = 90.
- Hence K, A, L are colinear.
- Similarly, L, B, J are colinear and J, C, K are colinear
- Prove that I is in-center of triangle ABC
- AJ is bisector of angle A.
- BK is bisector of angle B.
- CL is bisector of angle C.
- Hence I is in-center of triangle ABC.
- Prove that I is olso the orthocenter of triangle JKL
- AJ is height of side KL.
- BK is height of side LJ.
- CL is height of side JK.
- Hence I is also the orthocenter of triangle JKL.
Q3. What is pedal triangle ?
Defintion
- The height JA with foot at A.
- The height KB with foot at B.
- The height LC with foot at C.
- Three feet of triangle JKL make a triangle ABC.
- Triangle ABC is called pedal triangle of JKL.
Properties
- In-center of pedal traingle JKL is the orthocenter of triangle JKL.
Q4. Reference
- Ex-central triangle : MD2002 13 03.
- Pedal triangle : MD2002 13 02.
|