Q1. Theory 1
- A and B are fixed points and C is a moving point
- If angle ACB keeps 90 degrees, the locus of C is a circle
- and AB is the diameter.
Q2. Theory 2
- A and B are fixed points and C is a moving point
- If angle ACB keeps constant, the locus of C is an arch
- and AB is the chord of a circle.
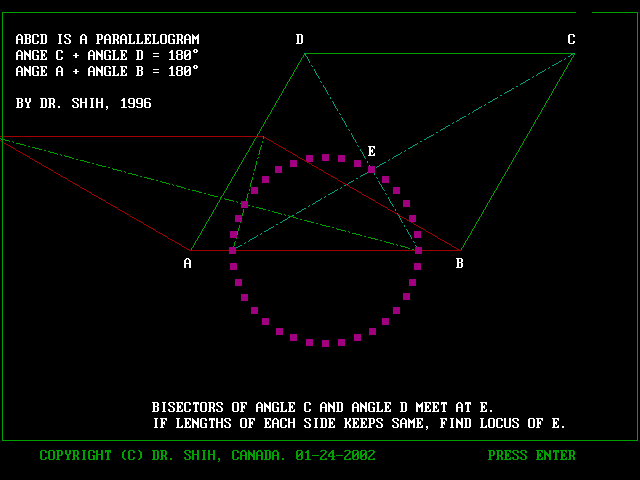
Q3. The question is given as below
- parallelogram ABCD : A,B are fixed points and AB=fiexd length
- C and D can move but BC and DA are fixed length.
- Angle C has bisector and meets AB at point P
- Angle D has bisector and meets AB at point Q
- Bisectors CP and DQ meet at E
- If C and D move, what is the locus of E ?
A1. It is circle.
Q4. How to prove ?
- The angle bisectors meets the base AB at points P and Q
- Prove that angle PEQ=90 degrees
- Angle CPB = angle PCD = C/2
- Angle AQD = angle QDC = D/2
- Angle PEQ = pi - angle CPB - angle AQD
- Angle PEQ = pi - (C+D)/2 = 90 degrees
- The angle PEQ is constant and equal 90 degrees
- Prove that P and Q are fixed points
- Triangle PBC : PB = BC = fixed length
- Triangle AQD : AQ = AD = fixed length
- Hence P and Q are fixed points
- By theory 1, we know that locus of E is circle
- Hence locus of E is a circle
Q5. Demo of this locus is given in MD2002 ZM02 program 14
|