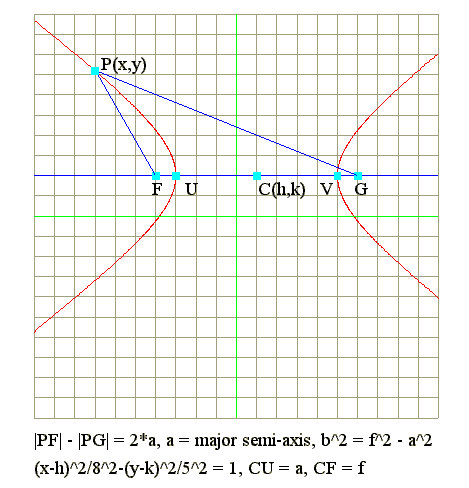
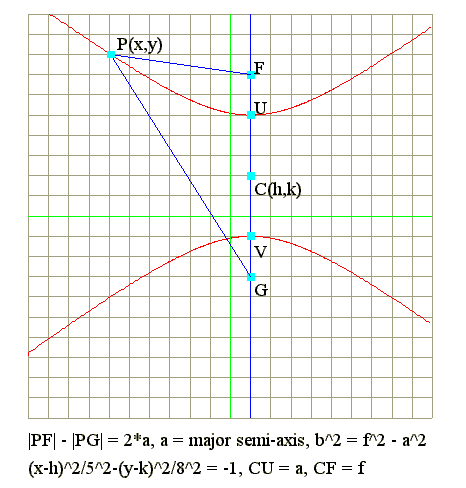
Q1. Defintion : |PF| - |PG| = 2*a is hyperbola
- If |PF| - |PG| = 2*a, then the locus of P is hyperbola.
- Equation of locus : (x-h)^2/a^2 - (y-k)^2/b^2 = 1.
- Center is at C(h,k).
- CF = CG = f = focal length = Sqr(a^2 + b^2).
- CU = CV = a = major semi-axis.
- FU = CF - CU = f - a.
- Principal axis is y = k.
Q2. Definition : R/PQ = e is ahyperbola in polar coordiante
- Equation of locus is R = D*e/(1-e*cos(A)) when e > 1.
- Where focus F is (0,0) and angle A is PF making with x-axis.
- Directrix is y = -D where D is the distance from F to direcrtix.
- PQ is distance from P to directirx and Q is on directrix.
- R = PF and PQ = D + x where x = R*cos(A).
- e = f/a and e is greater than 1 for hyperbola.
Q3. How to find D ?
- Since e = f/a.
- When A 180 and cos(A) = -1.
- Hence R = UF = D*e/(1+e) = f - a.
- Hence D = (f-a)*(1+e)/e
Example : x^2/4^2 - y^2/3^2 = 1. Find equation of directrix.
- Principal axis is y = 0.
- a=4 and b=3. Hence f = Sqr(a^2+b^2) = 5
- e = f/a = 5/4 = 1.25.
- Use polar form : R = D*e/(1-e*cos(A)) and F is the origin.
- When A = 180 and con(A) = -1 and R = UF = a - f.
- Hence f - a = D*e/(1+e).
- Hence D = (f-a)*(1+e)/e = (5-4)*(1+1.25)/1.25 = 1.8.
- Hence equation of directrix is x = -f - D = -6.8.
- Use polar form : R = D*e/(1+e*cos(A)) and F is the origin.
- When A = 0 and con(A) = 1 and R = VG = f - a.
- Hence f - a = D*e/(1+e).
- Hence D = (f-a)*(1+e)/e = (5-4)*(1+1.25)/1.25 = 1.8.
- Hence equation of directrix is x = f + D = 6.8.
|