-
Symbol Defintion
Example : Sqr(x) = square root of x
Q01. Diagram and question
|
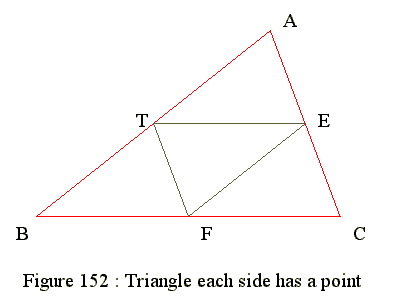
Diagram : Triangle ABC divide into 4 triangles
- Draw a triangle ABC and sides are a,b,c
- Let E be mid point on AC and CE = AE = b/2
- Let T be mid point on BA and BT = TA = c/2
- Let F be mid point of BC and BF = CF = a/2
- Join ET, TF and FE so that make four triangles
- 1. Prove that area of triangle EFT = (area of triangle ABC)/4
- 2. Prove that area FEC = area EAT = area TBF = area EFT
- 3. Area of triangle EFT = (R^2)*sin(A)*sin(B)*sin(C)/2
- 4. Join mid points of triangle and form 4 congruent triangle
Go to Begin
Q02. Area of triangle and sine law
Sine law
- a = 2*R*sin(A)
- b = 2*R*sin(B)
- c = 2*R*sin(C)
- = b*c*sin(A)/2
- = c*a*sin(B)/2
- = a*b*sin(B)/2
- = b*c*sin(A)/2 = b*c*(a/(2*R))/2 = a*b*c/(4*R)
- = c*a*sin(B)/2 = c*a*(b/(2*R))/2 = a*b*c/(4*R)
- = a*b*sin(B)/2 = a*b*(c/(2*R))/2 = a*b*c/(4*R)
- = a*b*c/(4*R) = 2*(R^2)*sin(A)*sin(B)*sin(C)
Go to Begin
Q03. Area EFT = a*b*c/(16*R) = (R^2)*sin(A)*sin(B)*sin(C)/2
Find area FEC, EAT and TBF
- Area FEC
- Area = (b/2)*(a/2)*sin(C)/2
- Area = a*b*sin(C)/8
- Area = (R^2)*sin(A)*sin(B)*sin(C)/2
- Area = a*b*c/(16*R)
- Area EAT
- Area = (b/2)*(c/2)*sin(A)/2
- Area = b*c*sin(A)/8
- Area = (R^2)*sin(A)*sin(B)*sin(C)/2
- Area = a*b*c/(16*R)
- Area TBF
- Area = (c/2)*(a/2)*sin(B)/2
- Area = c*a*sin(B)/8
- Area = (R^2)*sin(A)*sin(B)*sin(C)/2
- Area = a*b*c/(16*R)
- Area = area ABC - (area FEC + area EAT + area TBF)
- Area = (2 - 3/2)*(R^2)*sin(A)*sin(B)*sin(C)
- Area = (R^2)*sin(A)*sin(B)*sin(C)/2
- Since Area FEC = area EAT = area TBF = area EFT
- Since Area ABC = Area FEC + area EAT + area TBF + area EFT
- Hence are EFT = (area ABC)/4
- Area ABC = a*b*c/(4*R)
- Area EFT = (R^2)*sin(A)*sin(B)*sin(C)/2
- = (R^2)*(a/(2*R))*(b/(2*R))*(c/(2*R))/2
- = a*b*c/(16*R)
- = (Area ABC)/4
Go to Begin
Q4. Prove area EFT = (Area ABC)/4 geometrically
Proof
- Since T and E are mid points
- Hence TE = BC/2 and TE parallel to BC
- Hence angle EBT = angle ETA
- BT = TA and TE = BF
- Hence triangle EBT is congruent to triangle ETA (SAS)
- Similarly triangle ETA is congruent to trangle EFC
- Triangle EFT is congruent to triangle BFT (SAS)
- EF = BT
- TE = BF
- Since BFET is parallelogram
- Hence angle FBT = angle FET
- Hence area EFT = (area ABC)/4
Go to Begin
