-
Symbol Defintion
Example : Sqr(x) = square root of x
Q01. Diagram of y = (x - 1)^3/(2*x)
The diagram of Y=((x-1)^3)/(2*x) 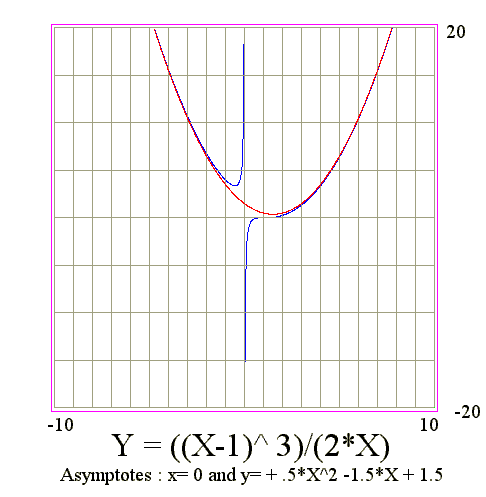
|
Go to Begin
Q02. Definition of asymptotes
Deifintion
-
1. Vertical asymptote ...... x = a if f(a) = ∝
2. Horizontal asymptote .... y = b if f(x)=b as x = ∝
3. Oblique asymptote ....... y = F(x) when x = ∝
Go to Begin
Q03. Find asymptote of y=((x-1)^3)/(2*x)
Sketch program
-
* Find the diagram of y=(x-1)^3/(2*x)
* On internet : Program ABH
* Click Program ABH Program 03 03
-
* Run program ABH
* Click Demo
* Click Topic 3 in upper box
* Click program 03 04 in lower box
Go to Begin
Q4. Find signs of y' and y" from diagram
Asymptotes
- We get Vertical asymptote : x=0 and y=infinite
- We get Oblique asymptote : y=(x^2-3*x+3)/2 and x=infinite
- We can estimate the extreme points if y' = 0
- We can get the point of inflexion if y" = 0
Go to Begin
Q5. Find zero, critical points and inflextion of y = ((x-1)^3)/(2*x)
Solution
- Value of zero : x1 = 1 and y = 0
- Critical points at y'=0
- y'=(3*(x-1)^2)*(2*x)) - 2*(x-1)^3)/(4*x^2)
- y'=((x-1)^2)*(6*x-2*(x-1))/(4*x^2)
- y'=((x-1)^2)*(4*x+2))/(4*x^2)
- y'=0 and x2=1 or x3=-1/2
- Critical point is at x3=-1/2
- Point of inflextion at y"=0
- y" = ?
- y" = 0 at x2 = 1
- Point of inflextion at x2 = 1
Go to Begin
Q6. Properties of y = ((x - 1)^3)/(2*x)
Answer
- y-intercept : None
- Signs of y
- Domain x < 0 : y is positive
- Domain x = 0 : No exist and it has asymptote
- Domain x between 0 and 1 : y is negative
- Domain x > 1 : y is positive
- Signs of y'
- Domain x < x3 : The curve is decreasing (y' less than 0)
- Domain x3 < x < 0 : The curve is increasing (y' greater than 0)
- Domain at x = x3 : It is a minimum point (y'=0)
- No domain at x=0 (asymptote)
- Domain x greater than 0 curve is increasing (y' greater than zero)
- Signs of y"
- Domain x less than 0 curve concave upward (y" is positive)
- Domain between 0 and x = 1 curve concave downward (y" is negative)
- Domain at x greater then 1 curve concave upward (y" is positive)
- Domain at x = 1 it is point of inflextion (y" = 0)
- Range : y=-infinite to y=positive infinite
- For large abs(x) the curve approaches a parabola (aymptote)
Go to Begin
