-
Symbol Defintion
Sqr(x) = Square root of x
Q01. Study y = 1/x
Keywords
- Hyperbola
- First and send derivative
- If x LT 0
- When x goto -infinite, y EQ -0. Hence y = 0 is horizontal asymptote
- The range of y is from -0 to -infinite at x = 0
- The curve is decreasing (y' = -1/(x^2) is less than zero)
- The curve is concave downward (y" = 2/(x^3) is less than zero)
- If x EQ 0
- The curve goes to -infinite
- Hence x = 0 is vertical asymptote
- If x GT 0
- When x goto +infinite, y EQ +0. Hence y = 0 is horizontal asymptote
- The range of y is from +infinite at x = 0 to +0
- The curve is decreasing (y' = -1/(x^2) is negative)
- The curve is concave upward (y" = 2/(x^3) is positive)
- It has no y-intercept and no zero values
- Prove that y = 1/x is a hypebola
- Use discriminat of F(,x,y) : B^2 - 4*A*C
- For x*y = 1, A = 0, B = 1 and C = 0.
- Hence B^2 - 4*A*C = 1 and the graph is a hyperbola
- Prove that the semi-axis is a = b = Sqr(2) : See AN 14 02
- Find focal length : f = Sqr(a^2 + b^2) = 2
- The equation of principal axis : y = -x
- Find coordinate of vertices
- U is at x = +1 and y = +1
- V is at x = -1 and y = -1
- Find coordinate of foci
- F is at (+Sqr(2), +Sqr(2))
- G is at (-Sqr(2), -Sqr(2))
- Find equation of directrix
- (x/a)^2 - (y/b)^2 = 1 and a = b = Sqr(2) and f = 2
- e = f/a = 2/Sqr(2) = Sqr(2)
- R = D*e/(1 - e*cos(A))
- When angle A = 180, R = f - a = D*e/(1 - e*cos(180))
- Hence (f - a) = D*e/(1 + e)
- Hence D*e = (f - a)*(1 + e)
- Hence D*Sqr(2) = (2 - Sqr(2))*(1 + Sqr(2))
- Hence D = (Sqr(2) - 1)*(1/Sqr(2) + 1)
- Hence D = (0.4142)*(1.7071) = 0.7071 from focus F or G along y = x
- Find D on y = x
- D from center (0,0) is DD = f - D = 2 - 0.7071 along y = x
- In oxy coordiante directrix passing (xd,yd)
- xd = DD*cos(45) = (2 - 0.7071)*cos(45) = 0.5 or -0.5
- yd = DD*sin(45) = (2 - 0.7071)*sin(45) = 0.5 or -0.5
- The slope of directrix is S = -1
- Hence equation of directix is y = s*x + c
- -0.5 = (-1)*(-0.5) + c
- c = -1
- Hence y = -x - 1 is the equation
- The asymptotes : y = 0 and y = 0
- Diagram with directrix
-
Diagram
Fig01. 04 05
-
Diagram
Fig01. 04 05
- Diagram : AN 21 : 14 04
- Text : AN 14 02
- Hyperboba : AN 08 00
Go to Begin
Q02. Prove that cos(A-B) = cos(A)*cos(B) + sin(A)*sin(B)
Keywords
- Distance formula
- Cosine law
Go to Begin
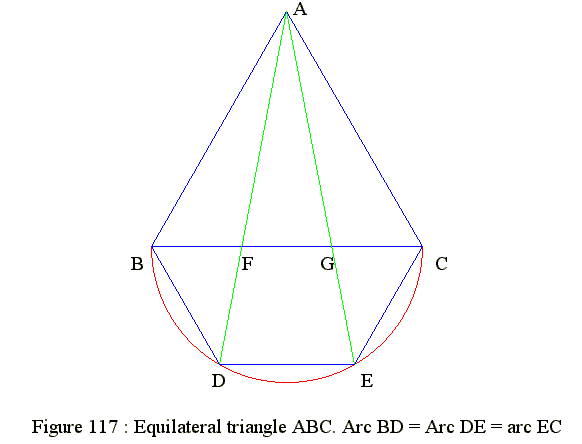
Q03. Equilateral triangle : Divide one side into 3 equal parts
Keywords
- Properties of equilateral triangle
- Properties of hexagon
- Law of cosine and law of sine
- Draw an equilateral triangle ABC
- Use BC as diameter to draw a semi-circle below BC
- Divide the semi-circle into 3 equal arcs : Arc BD = arc DE = arc EC
- Join AD and cut BC at F
- Join AE and cut BC at G
- Then BF = FG = GC
- Let BC = AB = 2 then BD = 1
- It is known that angle ABD = 120 degrees (Angle ABF = 60, angle FBD = 60)
- In triangle ABD, find AD by cosine law
- We know AB = 2, angle ABD = 120 and BD = 1.
- AD^2 = AB^2 + BD^2 - 2*AB*BD*cos(ABD)
- AD^2 = 2^2 + 1^2 - 2*2*1*cos(120)
- AD^2 = 5 - 4*(-1/2)
- AD^2 = 7 or AD = Sqr(7)
- In triangle ABD, we can find angle BAD by sine law
- BD/sin(BAD) = AD/sin(ABD)
- Hence sin(BAD) = BD*sin(ABD)/AD
- Hence sin(BAD)
- = 1*sin(120)/Sqr(7)
- = (Sqr(3)/2)/(Sqr(7))
- = Sqr(3)/(2*Sqr(7) ............... (1)
- cos(BAD) = Sqr(1 - sin(BAD)^2)
- = Sqr(1 - 3/28)
- = 5/Sqr(28) ...................... (2)
- In right triangle AOF where AO perpendicular to BC, find AF
- AO = Sqr(3)
- Angle FAO = 30 - angle BAF
- cos(FAO) = cos(30 - BAF)
- = cos(30)*cos(BAF) + sin(30)*sin(BAF)
- Substitute (1) and (2) into above expression
- cos(FAO) = (Sqr(3)/2)*(Sqr(25/28)) + (1/2)*(1/(2*Sqr(7))
- = (5*Sqr(3)/(2*Sqr(28)) + 1/(4*Sqr(7))
- = (5 + 1)/(4*Sqr(7))
- = 3/(2*Sqr(7)) ............................. (3)
- Since triangle is right triangle
- hence AF = AO/cos(FAO)
- Substitute into above we have
- AF = (Sqr(3)*2*Sqr(7))/3 = 2*Sqr(21)/3 ..... (4)
- In triangle ABF, we use sine law again to find BF
- BF/sin(BAF) = AF/sin(60)
- Substitute (1) and (4) into above expression
- BF = (1/(2*Sqr(7))*(2*Sqr(21)/3)/(Sqr(3)/2)
- = (2*Sqr(21)/(6*Sqr(7))/(Sqr(3)/2)
- = (4*Sqr(21))/(6*Sqr(21))
- = 2/3
- = BC/3 where we assume BC = 2
Go to Begin
Q04. Study y = (x^2)/2 - 1
Diagram
-
Diagram
Fig. 02 01
- 1. y-intercept is c = -1
- 2. Zero values are at x1 = +Sqr(2) and x2 = -Sqr(2)
- 3. When x LT 0, the curve is decreasing (y' LT 0)
- 4. When x GT 0, the curve is increasing (y' GT 0)
- 5. The curve is concave upward (a GT 0 or y" GT 0)
- 6. Vertex at (0, -1). It is the minimum point
- 1. Principal axis is x = 0
- 2. Vertex is at xv = 0 and yv = -1
- 3. Distance from focus to vertex is D = 1/(2*a) = 2
- 4. Vertex is at mid point from focus to directrix
- Focus : xf = xv = 0 amd yf = yv + D/2 = -1 + 1 = 0
- Equation of diectrix : y = yv - D/2 = -2
- 5. Locus : Point P to focus and directrix has same diatance
- 6. Polar form : y = D/(1 - sin(A)) and D = 2
Go to Begin
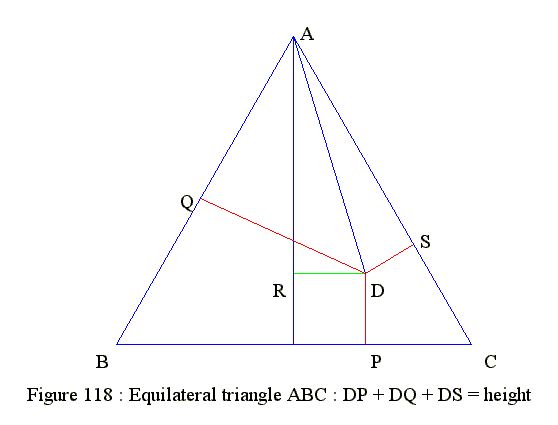
Q05. Equilateral triangle : DP + DQ + DS = height
Keywords
- Equilateral triangle properties
- sin(A) + sin(B) = 2*sin((A+B)/2)*cos((A-B)/2)
- 1. Draw an equilateral triangle
- 2. Point D is inside triangle
- 3. Draw DP, DQ and DS perpendicular to the sides
- 4. Prove that DP + DQ + DS = h
- Angle BAD = 30 + angle RAD and Angle DAQ = 30 - angle RAD
- Right triangle ADQ : DQ = AD*sin(30 - RAD)
- Right triangle SAD : DS = AD*sin(30 + RAD)
- Hence DQ + DS = AD*(sin(30 - RAD) + sin(30 + RAD))
- Since sin(A) + sin(B) = 2*(sin((A+B)/2)*(cos(A-B)/2)
- Hence DQ + DS = 2*AD*(sin(30)*cos(RAD))
- = AD*cos(RAD)
- = AR
- Height = AR + DP = DP + DQ + DS
Go to Begin
Q06. A(7,4), B(3,1), C(0,k) if AC + BC is minimum find k
Keywords
- y is minimu if y' = 0
- if y = a*x^2 + b*x + c, y' = 2*a*x + b
- If y = Sqr(a*x^2 + b*x + c), y' = (2*a*x + b)/(2*Sqr(a*x^2 + b*x + c)
- 1. Draw rectangular coordinate
- 2. Draw points A, B and C
- Let h = AC + BC
- = Sqr((7 - 0)^2 + (4 - k)^2) + Sqr((3 - 0)^2 + (1 - k)^2)
- = Sqr(49 + 16 - 8*k + k^2) + Sqr(9 + 1 - 2*k + k^2)
- = Sqr(k^2 - 8*k + 65) + Sqr(k^2 - 2*k + 10)
- If h is minimum
- dh/dk = 0
- (2*k - 8)/(2*Sqr(k^2 - 8*k + 65)) + (2*k - 2)/(2*Sqr(k^2 - 2*k + 10)) = 0
- Simplify, we have
- (k - 4)*Sqr(k^2 - 2*k + 10) = -(k - 1)*Sqr(k^2 - 8*k + 65)
- Square both sides
- ((k - 4)^2)*(9 + (k - 1)^2) = ((k - 1)^2)*(49 + (k^2 - 4)^2)
- 9*(k - 4)^2 + ((k - 4)*(x - 1))^2 = 49*((k - 1)^2) + ((k - 1)*(x^2 - 4))^2
- 9*(k - 4)^2 = 49*(k - 1)^2
- Take square on both sides
- 3*(k - 4) = +7*(k - 1), 4*k = -5 or k = -1.25
- 3*(k - 4) = -7*(k - 1), 10*k = 19 or k = 1.9
- h^2 = AC^2 + BC^2
- h^2 = (49 + (4 - k)^2) + (9 + (k - 1)^2)
- h^2 = 65 - 8*k + k^2 + 10 + k^2 - 2*k
- h^2 = 2*k^2 - 10*k + 75
- Use completing the square
- h^2 = 2*(k^2 - 5*k + (5/2)^2 - (5/2)^2) + 75
- h^2 = 2*(k - 5/2)^2 + 75 - 2*(5/2)^2
- h^2 is minimum if k = 5/2
- Use derivetative
- d(h^2)/dk = 0
- 4*k - 10 = 0
- k = 2.5
Go to Begin
Q07. Answer
Go to Begin
Q08. Answer
Go to Begin
Q09. Answer
Go to Begin
Q10. Answer
Go to Begin