Q01. Inverse function of y = a*x^2 + b*x + c
Definition
- 1. It is the reflection of Y = F(X) about Y = X
- 2. It is the image of Y = F(X) about Y = X (it looks like mirror)
- 3. The inverse is x = a*y^2 + b*y + c
- Y = F(X) and find X interms of Y
- That is to interchange X and Y as X = F(Y)
Go to Begin
Q02. Inverse of Y = a*x^2 + b*x + c is X = a*y^2 + b*y + c
Find the inverse
- Solve for x and we have x = (-b + Sqr(b^2-4*a*(c-y))/(2*a)
- The inverse is y = (-b + Sqr(b^2-4*a*(c-x))/(2*a)
- The inverse is y = (-b - Sqr(b^2-4*a*(c-x))/(2*a)
- The inverse is x = a*y^2 + b*y + c
- 2*a*y + b = Sqr(b^2 - 4*a*(c-x))
- Square both sides : (2*a*y + b)^2 = b^2 - 4*a*(c-x)
- 4*a^2*y^2 + 4*a*b*y + b^2) = b^2 - 4*a*c + 4*a*x
- 4*a*x = 4*a^2*y^2 +4*a*b*y + 4*a*c
- x = a*y^2 + b*y + c
Go to Begin
Q03 Find intersection of y = a*x^2 + B*x + c with it inverse
How many intersctions of y = a*x^2+b*x+c with its inverse
- There is no intersection
- There is one intersection
- There are two intersections
- There are four intersections
-
* Find intersection of y = a*x^2 + b*x + c with inverse
* First we solve y = a*x^2 + b*x + c and y = x
* This gives a quadratic equation : a*x^2 + (b-1)*x + c = 0
* Let Discriminant D = (b - 1)^2 - 4*a*c
* D < 0 then there is no intersection
* D = 0 there is one intersection, i.e. y = x is tangent to curve
* D > 0 there are 2 or 4 intersections
Go to Begin
Q04 Find intersection of y = x^2 - 6*x + 8 with it inverse
Funtion y = a*x^2 + b*x + c and its inverse has 4 intersections
- Since (b - 1)^2 - 4*a*c GT 0, It has at least two intersections
- we have to solve a quartic equation to find other two
- Substitute y = a*x^2 + b*x + c into x = a*y^2 + b*y + c
- x = a*(a*x^2+b*x+c)^2 + b*(a*x+b*y+c) + c = 0
- Expand above equation we get a quartic equation
- How to solve the quartic equation
- We alreay have two solutions for this quartic equation
- They are the solutions of y = a*x^2 + b*x + c and y = x
- Let the two sultion be r and s
- Then we have two methods to solve the quartic equation
- One method is using synthetic division
- Other one is using the relation of roots and coefficients
- Since (b - 1)^2 - 4*a*c = (-6 - 1)^2 - 4*1*8 = 15
- Hence it has 2 or 4 points of intersections
- Solution
- x = x^2 - 6*x + 8
- x^2 - 7x + 8 = 0
- x1 = (7 + Sqr(49 - 4*1*8))/2 = (7 + Sqr(17))/2 = 5.56155
- x2 = (7 - Sqr(49 - 4*1*8))/2 = (7 + Sqr(17))/2 = 1.4395
- Substitute y = x^2 - 6*x + 8 into x = y^2 - 6*y + 8
- x = (x^2 - 6*x + 8)^2 - 6*(x^2 - 6*x + 8) + 8
- x = x^4 - 12*x^3 + 46*x^2 - 60*x - 40
- x^4 - 12*x^3 + 46*x^2 - 61*x + 24 = 0
- Solve this quartic equation by using x1 and x2
- Sum of roots = -coeff of x^3
- Then we can get x1 + x2 + x3 + x4 = -(-12) .......... (1)
- Substitute x1 and x2 into (1) : x3 + x4 = 5.0000 .... (2)
- Product of roots = constant term
- x1*x2*x3*x4 = 24 .................................... (3)
- Substitute x1 and x2 into (3) : x3*x4 = 2.99781 ..... (4)
- Solve (2) and (4) we have x^2 - 5*x + 2.99781 = 0
- x3 = (5 + Sqr(25 - 4*2.99781))/2 = (5 + 3.60676)/2 = 4.30338
- x4 = (5 - 3.60678)/2 = 0.69661
- x1 = 5.56 and y1 = (5.56)^2 - 6*5.56 + 8 =
- x2 = 1.44 and y2 = (1.44)^2 - 6*1.44 + 8 =
- x3 = 4.30 and y3 = (4.30)^2 - 6*3.62 + 8 =
- x4 = 0.69 and y4 = (0.69)^2 - 6*1.39 + 8 =
-
Graphic Calculater Section 6 10
- Start the program
- Select 6 in upper box
- Select 10 in lower box
- Give coefficients 1, -6, 8
Go to Begin
Q05 Diagram of intersection of y = x^2 - 6*x + 8 with it inverse
|
y = x^2 - 6*x + 8 and its inverse 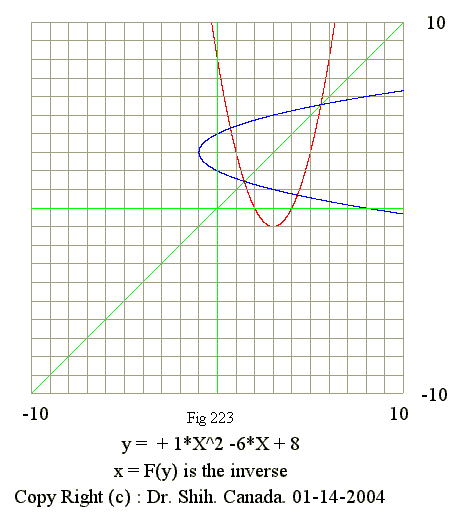
y = x^2 + 0.25 and its inverse 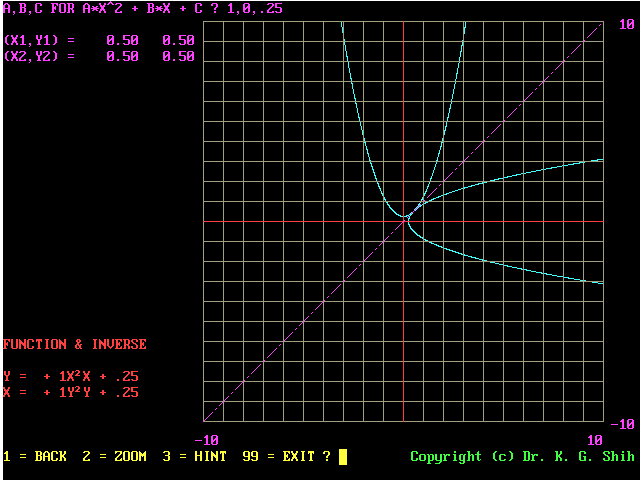
|
Go to Begin
