-
Symbol Defintion
Example : Sqr(x) = square root of x
Q01. Diagram : Proof of sine law
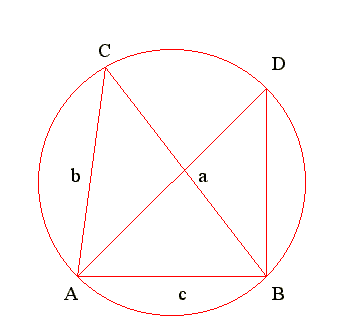
|
Go to Begin
Q02. Sine Law
Outlines : Sine law.
- Triangle ABC
- Angles A,B and C .
- sides a = BC, b = CA and c = AB.
- Defintion of sine law
- Triangle ABC : a/sin(A) = b/sin(B) = c/sin(C) = 2*R.
- Where R is theradius of circum-circle.
- Application : Solve triangle to find another angles and sides
- SAA : Solve triangle if a, A, B are given.
- SSA : Solve triangle if a, b, A are given.
- Construction
- Draw a circle of radius R.
- Draw triangle inscribed in the circle.
- Draw diameter AD and formed triangle ADB.
- Proof
- Angle ABD = 90 degrees.
- Hence sin(ADB) = AB/AD = c/(2*R)
- Angle ADB = angle ACB = C.
- Hence sin(C) = c/(2*R)
- Hence c/Sin(C) = 2*R.
- Similarly, a/sin(A) = 2*R and b/sin(B) = 2*R
- Triangle Area = b*c*sin(A) = c*a*sin(B) = a*b*sin(C).
- Divide by abc.
- Hence sin(A)/a = sin(B)/c = sin(C)/c.
Go to Begin
Q03. Area of triangle = a*b*c/4
Hint : It requires
- 1. Sine law : a = 2*R*sin(A), b = 2*R*sin(B) and c = 2*R*sin(C)
- 2. Area of triangle = a*b*sin(C)/2
- Area of triangle = a*b*sin(C)/2
- sin(C) = c/(2*R)
- Hence area of triangle = a*b*c/(4*R)
- Where R is radius of circum-circle
Go to Begin
Q04. Area of triangle = 2*(R^2)*sin(A)*sin(B)*sin(C)
Hint : It requires
- 1. Sine law : a = 2*R*sin(A), b = 2*R*sin(B) and c = 2*R*sin(C)
- 2. Area of triangle = a*b*sin(C)/2
- Area of triangle = a*b*sin(C)/2
- a = 2*R*sin(A)
- b = 2*R*sin(B)
- Hence Area of triangle = 2*(R^2)*sin(A)*sin(B)*sin(C)
Go to Begin
Q05. Solve triangle if SSA or SAA are given
Given that A = 30, a = 4 and b = 6. Find B, C and c.
- Using sine law
- Sin(A)/a = sin(B)/b
- Hence sin(B) = b*sin(A)/a = 6 *sin(30)/4 = 1.5*(1/2) = 0.75.
- Hence B = 48.59 degrees.
- C = 180 - A - B = 101.41.
- Sin(A)/a = sin(C)/c
- c = a*sin(C)/sin(A) = 4*sin(101.41)/sin(30) = 4*(0.980237)/(1/2) = 7.8419.
- sin(A)/a = sin(30)/4 = 1/8 = 0.125.
- sin(C)/c = sin(101.41)/7.6419 = 0.12499
Go to Begin
