Mathematics Dictionary
Sine and Cosine Functions
Questions

    Read Symbol defintion

  • Q01 | - First mathematical theory
  • Q02 | - Definition of sine function and cosine function
  • Q03 | - The Pythagorian theory
  • Q04 | - Sine and cosine functions in rectangular coordinates
  • Q05 | - The graph of y = sin(x) and y = cos(x) for x between -2*pi and 2*pi
  • Q06 | - Special angle 30, 45 and 60 degrees
  • Q07 | - Funtion and co-function in various quadrant
  • Q08 | - Related functions in various quadrants
  • Q09 | - Properties of y = sin(x) and y = cos(x)
  • Q10 | - Relation with other ratios
  • Q11 | - Formula related with sum of angles (A+B)
  • Q12 | - Trigonometric laws
  • Q13 | - Solve equations including sin(x) and cos(x)
  • Q14 | - Advanced formula
  • Q15 | - Inverse of y = sin(x) and y = cos(x)
  • Q16 | - Reference
  • Q17 | - Angle related with 18 degrees
  • Q18 | - Quiz for sine and cosine
  • Q19 | - Answer to Quiz for sine and cosine
Answers


Q01. First mathematical theory

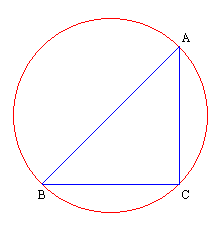
  • In the given Figure, AB is the diameter.
  • Then angle ACB is a right angle (pi/2).
  • This is the first mathematical theeory.
Go to Begin

Q02. Definition of sine function and cosine function
The trigonometry of Ptolemy had been based on the functional relationship between the chards of a circle and the central angles they subtended. The sine function is called the chord function. The change from whole chord to half chord took place in India. It is believed that the word "sine" is the translation of Hindu name "Jiva". The definition of sine function and cosine in right triangle ABC (See Figure) is given as below :
  • In the given Figure ABC is right angle triangle.
  • Opp = BC is the opposite side of angle A.
  • Adj = AC is the adjacent side of angle A.
  • Hyp = AB is the hypothesis of the triangle.
  • Then
    • sin(A) = Opp/Hyp = BC/AB.
    • cos(A) = Adj/Hyp = AC/AB.
  • Hence they are originally called chord function.
Go to Begin

Q03. The Pythagorian theory

If we draw a circle and an inscribed triangle whose one side passes through the center, then we will that one chord is related to the sine function and the other chord is related to the cosine function. Hence the sine function and cosine function are related with two chords of a circle.
  • Sin(A) = BC/AB.
  • Cos(A) = AC/AB.
  • Since AC^2 + BC^2 = AB^2.
  • Hence we have Cos(A)^2 + Sin(A)^2 = 1.
  • This is called Pythagorean relation in trigonometry.
Go to Begin

Q04. Sine and cosine functions in rectangular coordinates

  • In 1st quadrant
    • sin(A) = y/r = (+).
    • cos(A) = x/r = (+).
  • In 2nd quadrant
    • sin(A) = y/r = (+).
    • cos(A) = x/r = (-).
  • In 3rd quadrant
    • sin(A) = y/r = (-).
    • cos(A) = x/r = (-).
  • In 4st quadrant
    • sin(A) = y/r = (-).
    • cos(A) = x/r = (+).
Go to Begin

Q05. The graph of y = sin(x) for x between -2*pi and 2*pi
A5. See ABH program 04 01 and find properties
  • Period is 2*pi.
  • Range : between -1 and +1.
  • Zeros : x = -2*pi, -pi, pi and 2*pi.
  • Find domain for the function is increasing.
  • Find domain for the function is decreasing.
  • Find domain for the function has critical points.
    • Maximum value = 1 at -3*pi/2 and pi/2. General solution = 2*n*pi + pi/2.
    • Minimum value =-1 at -pi/2 and 3*pi/2. General solution = 2*n*pi - pi/2.
  • Find domain for the function is concave downward.
  • Find domain for the function is concave upward.
  • Find domain for the function has point of inflexion at x = -pi, 0, and pi.
The graph of y = cos(x) for x between -2*pi and 2*pi
See ABH program 04 02 and find properties
  • Period is 2*pi.
  • Range : between -1 and +1.
  • Zeros : x = -1.5*pi, -0.5*pi, 0.5*pi, 1.5*pi.
  • Find domain for the function is increasing.
  • Find domain for the function is decreasing.
  • Find domain for the function has critical points.
    • Maximum value = 1 at -2*pi and 0 and 2*pi. General solution = 2*n*pi.
    • Minimum value =-1 at -pi and pi. General solution = 2*(n+1)*pi.
  • Find domain for the function is concave downward.
  • Find domain for the function is concave upward.
  • Find domain for the function has point of inflexion : x = -1.5*pi, -pi/, pi/2, 1.5*pi. .
Relation between graphs of y = sin(x) and y = cos(x)
  • Graph of y = cos(x) is identical to the graph of y = sin(x+ip/2).
  • Hence they have a phase differenc pi/2.
Go to Begin

Q06. Special angle 30, 45 and 60 degrees

Angle 30 degrees : Opp = Hyp/2 and Adj = Sqr(3)/2
  • sin(30) = Opp/Adj = 1/2.
  • sin(30) = Ady/Hyp = Sqr(3)/2.
Angle 45 degrees : Opp = Adj = 1 and Hyp = Sqr(2)
  • sin(45) = Opp/Adj = Sqr(2)/2.
  • sin(45) = Ady/Hyp = Sqr(2)/2.
Angle 60 degrees : Adj = 1 and Hyp = 2 Hence Opp = Sqr(3)
  • sin(60) = Opp/Adj = Sqr(3)/2.
  • sin(60) = Ady/Hyp = 1/2.
Proof of Sin(30)=1/2 Using right angle triangle
Go to Begin

Q07. Function and co-function

  • First quadrant
    • sin( 90-A) = +cos(A).
    • cos( 90-A) = +sin(A).
  • Second quadrant
    • sin( 90+A) = +cos(A).
    • cos( 90+A) = -sin(A).
  • Third quadrant
    • sin(270-A) = -cos(A).
    • cos(270-A) = -sin(A).
  • Fourth quadrant
    • sin(270+A) = -cos(A).
    • cos(270+A) = +sin(A).
Go to Begin

Q08. Relation of function in various quadrant

  • Second quadrant
    • sin(180-A) = +sin(A).
    • cos(180-A) = -cos(A).
  • Third quadrant
    • sin(180+A) = -sin(A).
    • cos(180+A) = -cos(A).
  • Fourth quadrant
    • sin(360-A) = -sin(A).
    • cos(360-A) = +cos(A).
  • First quadrant
    • sin(360+A) = +sin(A).
    • cos(360+A) = +cos(A).
Examples
  • cos(120) = cos(180-60) = -cos(60) = -1/2.
  • sin(330) = sin(360-30) = -sin(30) = -1/2.
Go to Begin

Q09. Properties of sine and cosine functions

Symmetry : Odd and even function
  • Odd function : F(-x) = -F(x)
    • Sin(-x) = -sin(x) and sine function is odd
  • Even function : F(-x) = F(x)
    • Cos(-x) = +cos(x) and cosine function is even
Period of function : F(x+p) = F(x) and p is period
  • y = sin(x) : period = 2*pi.
  • y = cos(x) : period = 2*pi.
Examples
  • y = sin(2*x) : period = 2*pi/2.
  • y = sin(3*x) : period = 2*pi/3.
  • y = sin(4*x) : period = 2*pi/4.
  • y = sin(n*x) : period = 2*pi/n.
Go to Begin

Q10. Relation with other ratios

  • Tan(x) = sin(x)/cos(x)
  • csc(x) = 1/sin(x)
  • sec(x) = 1/cos(x)
  • cot(x) = cos(x)/sin(x)
  • cos(x) = sqr(1-sin(x)^2) and sin(x) = sqr(1-cos(x)^2)
Go to Begin

Q11. Formula related with sum of angles (A+B)

    Sum and difference of two angles
    • sin(A+B) = sin(A)*cos(B) + cos(A)*sin(B)
    • sin(A-B) = sin(A)*cos(B) - cos(A)*sin(B)
    • cos(A+B) = cos(A)*cos(B) - sin(A)*sin(B)
    • cos(A-B) = cos(A)*cos(B) + sin(A)*sin(B)
    Multiple angles : based on sin(A+B) and let A = B
    • sin(2*x) = 2*sin(x)*cos(x)
    • sin(3*x) = 3*sin(x) - 4*sin(x)^3
    • cos(2*x) = cos(x)^2 - sin(x)^2
    Half angle : based on cos(2*x) = 2*cos(x)^2 - 1
    • cos(A/2) = abs(((1+cos(A))/2)
    • sin(A/2) = abs(((1-cos(A))/2)
    Product functions : Based on (A+B) and (A-B)
    • cos(A)*cos(B) = (cos(A+B)+cos(A-B))/2
    • cos(A)*sin(B) = (sin(A+B)-sin(A-B))/2
    • sin(A)*cos(B) = (sin(A+B)+sin(A-B))/2
    • sin(A)*sin(B) = (cos(A-B)-cos(A+B))/2
    Sum of functions : Based on product function
    • cos(A) + cos(B) = 2*(cos((A+B)/2) + cos((A-B)/2))
    • cos(A) - cos(B) = 2*(cos((A+B)/2) - cos((A-B)/2))
Go to Begin

Q12. Trigonometric laws

  • Sine law.
    • Trianle ABC : a/sin(A) = b/sin(B) = c/sin(C) = R
    • Where R is theradius of ex-circle.
    • Application
      • Solve triangle if a, A, B are given.
      • Solve triangle if a, b, A are given.
  • Cosine law.
    • Trianle ABC
      • a^2 = b^2 + c^2 - 2*b*c*cos(A).
      • b^2 = c^2 + a^2 - 2*c*a*cos(B).
      • c^2 = a^2 + b^2 - 2*b*c*cos(C).
    • Application
      • Solve triangle if b, A, c are given.
      • Solve triangle if c, B, a are given.
      • Solve triangle if a, C, b are given.
Go to Begin

Q13. Solve equations including sin(x) and cos(x)

General solutions
  • sin(x) = 1/2
    • Since sin(x) is positive, x is 1st or 2nd quadrant.
    • The principal solution in first quadrant is pi/6.
    • Hence x = 2*n*pi + pi/6 and x = 2*(n+1)*pi - pi/6.
  • sin(x) = -1/2
    • Since sin(x) is negative, x is 3rd or 4th quadrant.
    • The principal solution in first quadrant is pi/6.
    • Hence x = 2*n*pi - pi/6 and x = 2*(n+1)*pi - pi/6.
  • cos(x) = 1/2
    • Since cos(x) is positive, x is 1st or 4th quadrant.
    • The principal solution in first quadrant is pi/3.
    • Hence x = 2*n*pi + pi/3 and x = 2*n*pi - pi/3.
  • cos(x) = -1/2
    • Since sin(x) is negative, x is 2nd or 3rd quadrant.
    • The principal solution in first quadrant is pi/6.
    • Hence x = 2*(n+1)*pi - pi/6 and x = 2*(n+1)*pi + pi/6.
Go to Begin

Q14. Advanced formula
 Go to Begin

Q15. Inverse of sin(x) and y = cos(x)

Definition
  • if y = sin(x) then x = arcsin(y).
  • If y = cos(x) then x = arccos(y).
Composite function
  • sin(arcsin(x)) = x
  • cos(arccos(x)) = x
  • arcsin(sin(A)) = A
  • arccos(cos(A)) = A
Examples
  • Solve arcsin(-1/2) = x.
    • Since arcsin(-1/2) = x, hence sin(x) = -1/2.
    • Angle x is in 3rd or 4th quadrant.
    • In 3rd quadrant, x = 2*(n+1)*pi + pi/6.
    • In 4th quadrant, x = 2*n*pi = pi/6.
Go to Begin

Q16. Reference

  • MD2002 ZM20.exe : Trigonometry
  • MD2002 ZM21.exe : Trigonometry
  • MD2002 ZM22.exe : Trigonometry
  • MD2002 ZM31.exe : Related with chord
  • MD2002 ZS.txt : sine
  • MD2002 ZC.txt : Cosine
  • MD2002 ZT.txt : Trigonometry
Go to Begin

Q17. Angles related with 18 degrees

Find sin(18)
  • Let 5*x = 90 degrees.
  • Hence 3*x = 90 - 2*x.
  • Hence cos(3*x) = cos(90-2*x).
  • Hence -3*cos(x) + 4*cos(x)^3 = sin(2*x).
  • Hence -3*cos(x) + 4*cos(x)^3 = 2*cos(x)*sin(x).
  • Hence (-3 + 4*cos(x)^2 - 2*sin(x))*cos(x) = 0
  • Hence 4*cos(x)^2 - 2*sin(x) - 3) = 0
  • Hence 4*sin(x)^2 + 2*sin(x) - 1 = 0
  • Hence sin(x) = (-2 + Sqr(2^2 + 4*4*1))/(2*4) where x = 18 degrees.
Go to Begin

Q18. Quiz for sine and cosine

Angles in questions are in degrees
  • 1. If sin(x) = 1/2, find cos(x).
  • 2. Solve cos(x) = -1/2 for x between 0 and 360.
  • 3. Solve cos(x) = -1/2 in general solution.
  • 4. Solve sin(x) = 2.5.
  • 5. Solve arccos(2.55) = x.
  • 6. Find period of y = sin(4*x).
  • 7. Find value of sin(1100).
  • 8. Find value of arccos(cos(25.555)).
  • 9. Find value of sin(22.5) without calculator.
  • 10 Find value of sin(255) without calculator.
  • 11 Prove that sin(1)+sin(2)+sin(3)+......+sin(258)+sin(259).
  • 12 Prove that cos(1)+cos(2)+cos(3)+......+cos(178)+cos(179).
Go to Begin

Q19. Quiz for sine and cosine

Angles in questions are in degrees
  • 1. If sin(x) = 1/2, find cos(x).
    • cos(x) = +Sqr(1 - sin(x)^2) = +Sqr(3)/2 if x in 1st quadrant.
    • cos(x) = -Sqr(1 - sin(x)^2) = -Sqr(3)/2 if x in 2nd quadrant.
  • 2. Solve cos(x) = -1/2 for x between 0 and 360.
    • x is in 2nd and 4th quadrant.
    • Hence x = 180 - 60 = 120.
    • Hence x = 180 + 60 = 240.
  • 3. Solve cos(x) = -1/2 in general solution.
    • x is in 2nd and 4th quadrant.
    • Hence x = 2*(n-1)*pi - pi/3.
    • Hence x = 2*(n-1)*pi + pi/3.
  • 4. Solve sin(x) = 2.5.
    • Since sin(x) is between -1 and 1.
    • Hence there is no answer.
  • 5. Solve arccos(2.55) = x.
    • arccos(2.55) = x and cos(x) = 2.55.
    • Since cos(x) is between -1 and 1.
    • Hence there is no answer,
  • 6. Find period of y = sin(4*x).
    • Since y = sin(x) has period 2*pi.
    • Hence y = sin(4*x) has period 2*pi/4 = pi/2.
  • 7. Find value of sin(1100).
    • sin(1100) = sin(3*360+30) = sin(30) = 1/2.
  • 8. Find value of arccos(cos(25.555)).
    • arccos(cos(25.555)) = 25.555.
  • 9. Find value of sin(22.5) without calculator.
    • sin(22.5) = sin(45/2).
    • = Sqr((1-cos(45)^2)/2).
    • = Sqr((1-1/4)/2).
  • 10 Find value of sin(255) without calculator.
    • sin(255) = sin(180+75).
    • = -sin(75)
    • = -sin(30+45)
    • = -sin(30)*cos(45) - sin(45)*cos(30)
    • = -(1/2)*(Sqr(2)/2) - (Sqr(2)/2)*(Sqr(3)/2)
  • 11 Prove that sin(1)+sin(2)+sin(3)+......+sin(258)+sin(259).
    • sin(1) + sin(259) = sin(1) + sin(360-1) = sin(1) - sin(1) = 0.
    • sin(2) + sin(258) = sin(2) + sin(360-2) = sin(2) - sin(2) = 0.
    • sin(3) + sin(257) = sin(3) + sin(360-3) = sin(3) - sin(3) = 0.
    • .
    • .
    • sin(179) + sin(181) = sin(180+1) + sin(180+1) = sin(1) - sin(1) = 0.
    • sin(180) = 0
    • Hence the answer is 0.
  • 12 Prove that cos(1)+cos(2)+cos(3)+......+cos(178)+cos(179).
    • Same as quiz 11. The answer is zero.
Go to Begin
Show Room of MD2002 Contact Dr. Shih Math Examples Room
Copyright © Dr. K. G. Shih. Nova Scotia, Canada.
1