-
Read Symbol defintion
-
Q01 |
- Unit hyperbola
- Q02 | - Curve of x = tan(t) and y = sec(t)
- Q03 | - Prove the curve is concave downward when t = 180 to t = 270
- Q04 | - Diagrams of unit circle and unit hyperbola
- Q05 | - Comparison based on given diagrams
- Q06 | - Comparison based on given diagrams
- Q02 | - Curve of x = tan(t) and y = sec(t)
Q01. Unit hyperbola
Pythagorean relation
- 1 + tan(t)^2 = sec(t)^2
- If x = tan(t) and y = sec(t)
- Then 1 + x^2 = y^2
- Hence x^2 - y^2 = -1
- This is a hyperbola with principal axis y = 0
- 1 + tan(t)^2 = sec(t)^2
- If x = sec(t) and y = tan(t)
- Then 1 + y^2 = x^2
- Hence x^2 - y^2 = 1
- This is a hyperbola with principal axis y = 0
Go to Begin
Q02. Curve of x = tan(t) and y = sec(t)
Describe the curve when t is from 180 to 270
- From t = 180 to 270
- x = tan(t) = (+)
- y = sec(t) = (-)
- Hence the curve is in 4th quadrant
- When t = 180 or t = 270
- x = tan(180) = 0
- y = sec(180) = -1
- Hence the point is (0, -1)
- x = tan(270) = -infinite
- y = sec(270) = -infinite
- The curve is from (0,-1) decreasing to infinite
- The curve is concave downward as shown in diagram
Go to Begin
Q03. Prove the curve is concave downward when t = 180 to t = 270
Proof
- Find first derivative
- y' = dy/dx = (dy/dt)/(dx/dt)
- dy/dt = d/dt(tan(t)) = sec(t)^2
- dx/dt = d/dt(sec(t)) = sin(t)*(sec(t)^2)
- Hence y' = (sec(t)^2)/(sin(t)*(sec(t)^2))
- Hence y' = 1/sin(t)
- Since t is between 180 and 270, hence y' is negative
- Hence the curve is decreasing
- Find second derivative
- y" = d/dt(y')/(dx/dt)
- d/dt(y') = d/dt(1/sin(t)) = -cos(t)/(sin(t)^2) = -cos(t)*(csc(t)^2)
- Hence y" = -(cos(t)*(csc(t)^2))/(sin(t)*sec(t)^2)
- Hence y" = -cot(t)*(csc(t)/(sec(t))^2
- Since t is from 180 to 270, cot(t) is positive
- Hence y" is negative and the curve is concave downward
Go to Begin
Q04 Diagrams of unit circle and hyperbola
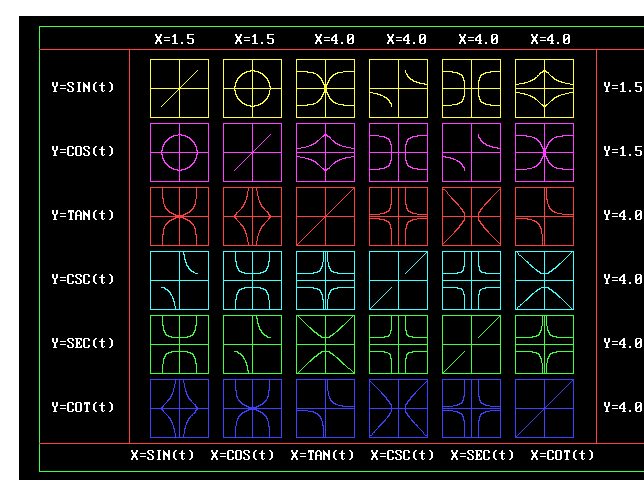
- 1. Find the curve of x = tan(t) and y = sec(t)
- 2. Find the curve of x = cot(t) and y = csc(t)
- 3. Find the curve of x = sec(t) and y = tan(t)
- 4. Find the curve of x = csc(t) and y = cot(t)
Go to Begin
Q05 Comparison by diagram
Use the diagrams to compare the following two parametric equations
- 1. Equation 1 : x = tan(t) and y = sec(t)
- 2. Equation 2 : x = cot(t) and y = csc(t)
- Based on the diagrams both are hyperbola with principal axis y = 0
- Henc no difference can be telled
Go to Begin
Q06 Comparison by trigonometric functions
Study the differencce of the following two parametric equations
- 1. Equation 1 : x = tan(t) and y = sec(t)
- 2. Equation 2 : x = cot(t) and y = csc(t)
- x = tan(t) and y = sec(t)
- t = 090 : x = -infinite 0 and y = -infinite
- t = 180 : x = 0 and y = -1
- Hence the curve is from infinte to (0, -1)
- Since x = (-) and y = (-)
- The curve is in 3rd quadrant
- The curve is concave downward
- The curve in xy coordinate : x from -infinite to 0 and y from -infinite to -1
- Hence the curve is increasing
- x = cot(t) and y = csc(t)
- t = 090 : x = 0 and y = 1
- t = 180 : x = -infinite and y = +infinite
- Hence the curve is from (-infinite, +infinite) to (0, 1)
- Since x = (-) and y = (+)
- The curve is in 2nd quadrant
- The curve is concave upward
- The curve in xy coordinate : x from -infinite to 0 and y from +infinite to 1
- Hence the curve is decreasing
- Hence the difference can be telled
- One is in 2nd quadrant and other in 3rd quadrant
