Q002 Solve x^4 + x^3 + x^2 + x + 1 = 0 using DeMoivre's theorem
Outlines
-
Q01 |
What is the DeMoivre theorem ?
- Q02 | How to solve x^5 - 1 = 0 using DeMoivre's theorem ?
- Q03 | Solve x^4 + x^3 + x^2 + x + 1 = 0
- Q04 | Diagram : Solve x^5 - 1 = 0
- Q05 | Solve x^5 - 1 = 0 by construction
- Q06 | Exercises
- Q07 | Reference
- Q02 | How to solve x^5 - 1 = 0 using DeMoivre's theorem ?
1. What is DeMoivre's Theorm ?
Find CIS(A)^n if n is positive integer
- (cos(A) + i*sin(A))^n = cos(n*A) + i*sin(n*A)
- (cos(A) + i*sin(A))^(1/n) = cos(k*pi*A/n) + i*sin(k*pi*A/n)
- Where k = 0,1,2,3,.... (n-1)
- CIS(A) = cos(A) + i*sin(A)
Go to Begin
2. Solve x^5 - 1 = 0 using DeMoivre's theorem
Method
- k = 0, r0 = cis(000) = cos(000) + i*sin(000) = +1
- k = 1, r1 = cis(072) = cos(072) + i*sin(072) = +0.3090 + i*9510
- k = 2, r2 = cis(144) = cos(144) + i*sin(144) = -0.3090 + i*9510
- k = 3, r3 = cis(216) = cos(216) + i*sin(216) = -0.3090 - i*9510
- k = 4, r4 = cis(288) = cos(288) + i*sin(288) = +0.3090 - i*9510
- r1 and r4 are conjugate complex roots
- r2 and r3 are conjugate complex roots
- Sum of the complex number is real
- Product of the complex number is also real
Go to Begin
3. Solve x^4 + x^3 + x^2 + x + 1 = 0 by construction
Method
- Since x^5 - 1 = (x - 1)*(x^4 + x^3 + x^2 + x + 1)
- Hence we can use the solution of x^5 - 1 = 0
- The roots are
- r1 = cis(72)
- r2 = cis(144)
- r3 = cis(216)
- r4 = cis(288)
Go to Begin
4. Diagram
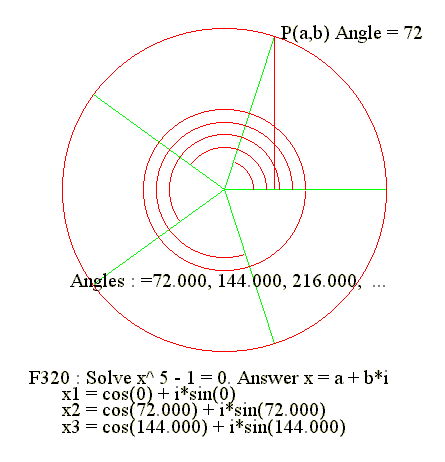
Go to Begin
5. solve x^5 - 1 = 0 by construction
Method
- Draw a large unit circle
- Draw angle A = 000 : r0 = x0 + i*y0 = 1
- Draw angle A = 072 : r1 = x1 + i*y1 = ?
- Draw angle A = 144 : r2 = x2 + i*y2 = ?
- Draw angle A = 216 : r0 = x3 + i*y3 = ?
- Draw angle A = 288 : r0 = x4 + i*y4 = ?
- x0 = 1 and y0 = 0
- x1 = ? and y1 = ?
- x2 = ? and y2 = ?
- x3 = ? and y3 = ?
- x4 = ? and y4 = ?
Go to Begin
6. Exercises
- Substitute cis(72) into x^5 - 1 = 0
- (cos(72) + isin(72))^5 - 1 = cos(5*72) + i*sin(5*72) - 1 = 1 - 1 = 0
- Hence cis(72) is a solution
- Similarly we can prove all of them
- Use equation theory for x^4 + x^3 + x^2 + x + 1 = 0
- The roots are cis(72), cis(144), cis(216) and cis(288)
- Since sum of roots = -coeff of x^3 = -1
- cos(72)+cos(144)+cos(216)+cos(288)+i*(sin(72)+sin(144)+sin(216)+sin(288))=-1
- cos(72)+cos(144)+cos(216)+cos(288) = -1
- Use equation theory for x^4 + x^3 + x^2 + x + 1 = 0
- The roots are cis(72), cis(144), cis(216) and cis(288)
- Since sum of roots = - coeff of x^3 = -1
- cos(72)+cos(144)+cos(216)+cos(288)+i*(sin(72)+sin(144)+sin(216)+sin(288))=-1
- sin(72)+sin(144)+sin(216)+sin(288) = 0
- Since r1 = +0.3090 + i*9510 is a root of x^5 - 1 = 0
- Hence (0.3090 + i*9510)^5 = 1
- Other method : (a + i*b) = a^5 + 5*(a^4)*(i*b) + 10*(a^3)*(i*b)^2 + ...
- Also we need i^5 = i, i^4 = 1, i^3 = -i, i^2 = -1
Go to Begin
7. Reference
Go to Begin
