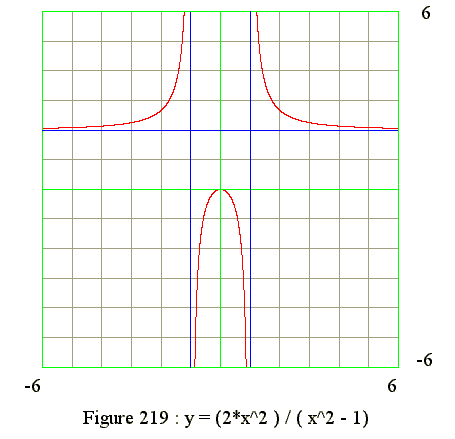
y = (2*x^2)/(x^2 - 1)
Q01. Diagram
|
Go to Begin
Q02. Cubic function has 3 zeros
Find y-intercept
- When x = 0 and y = 0
- Horizontal asymptote : When x = infinite and y = 2
- Vertical asymptotes :
- x = +1 and y = infinte
- x = -1 and y = infinite
- When x < -1
- y is positive and curve is in 2nd quadrant and y > 2
- x = -infinite and y = 2
- x = -1 and y = +infinite
- Hence the curve is increasing from (-infinite, 2) to (-1, infinite)
- Hence the curve is concave upward
- Hence y' is positive and y" is positive
- When x between -1 and 0
- x = -1 and y = -infinite
- x = 0 and y = 0
- Hence curve is increasing from (-1, -infinite) to (0,0)
- Hence curve is concave downward
- Hence y' is positive and y" is negative
- When x between 0 and 1
- x = 0 and y = 0
- x = 1 and y = -infinite
- Hence curve is decreasing from (0, 0) tp(1, -infinite)
- Hence curve is concave downward
- Hence y' is negative and y" is negative
- When x > 1
- y is positive and curve is in 1st quadrant and y >
- x = 1 and y = infinite
- x = infinite and y = 2
- Hence the curve is decreasing from (1, infinite) to (infinite, 2)
- Hence the curve is concave upward
- Hence y' is negative and y" is positive
Go to Begin
Q03. Find y'
First derivative y'
Go to Begin
Q04. Find y"
Second derivative y"
- y" =
Go to Begin
Q05. Discussion
Graphic solution
- The graphic solution is clear determine the signs of y, y' and y"
- The maximum and minimum points can only be estimated
Go to Begin