Figure 232 : 1 - cos(x) = Sqr(3)*sin(x)
-
Q01 |
- Diagram : Graphic solution of 1 - cos(x) = Sqr(3)*sin(x)
- Q02 | - Method 1 : Square both sides
- Q03 | - Method 2 : Use cos(A + B) = cos(A)*cos(B) - sin(A)*si(B)
- Q04 | - Method 3 : By observation
- Q05 | - Method 4 : Graphic solution of two curves
- Q06 | - Method 5 : Graphic solution of one curves
- Q02 | - Method 1 : Square both sides
Q01. Graph of y = 1 - cos(x) - Sqr(3)*sin(x)
|
Go to Begin
Q02. Method 1 : Square both sides
Solve 1 - cos(x) = Sqr(3)*sin(x)
- Square both side
- (1 - cos(x))^2 = (Sqr(3)*sin(x))^2
- 1 - 2*cos(x) + cos(x)^2 = 3*sin(x)^2
- Since cos(x)^2 + sin(x)^2 = 1
- Hence 1 - 2*cos(x) + cos(x)^2 = 3*(1 - cos(x)^2)
- Hence 4*cos(x)^2 - 2*cos(x) - 2 = 0 or 2*cos(x)^2 - cos(x) - 1 = 0
- Using quadratic formula we have
- Solution 1
- cos(x) = (-(-1) + Sqr((-1)^2 - 4*(2)*(-1))/(2*2) = (1 + 3)/4 = 1
- Hence x = 0 degrees.
- General solution is x = 2*n*pi
- Solution 2
- cos(x) = (-(-1) - Sqr((-1)^2 - 4*(2)*(-1))/(2*2) = (1 - 3)/4 = -1/2
- Hence x = 120 degrees.
- General solution is x = 2*n*pi + 2*pi/3
- Also cos(240) = -1/2, but x = 240 van not satisfy the equation
Go to Begin
Q03. Method 2 : Using cos(A - B) formula
Solve 1 - cos(x) = Sqr(3)*sin(x)
- Divide both side by 2, we have
- 1/2 - (1/2)*cos(x) = (Sqr(3)/2)*sin(x)
- Since cos(60) = 1/2 and sin(60) = Sqr(3)/2
- Hence cos(60)*cos(x) + sin(60)*sin(x) = 1/2
- Since cos(A - B) = cos(A)*cos(B) + sin(A)*sin(B)
- Hence cos(x - 60) = 1/2
- Solution 1
- Since cos(60) = 1/2 and hence x - 60 = 60
- x = 120 degrees and general solution is 2*n*pi + 2*pi/3
- Solution 2
- Since cos(300) = 1/2 and hence x - 60 = 300
- x = 360 or 0 degrees and general solution is 2*n*pi
Go to Begin
Q04. By observation
Solve 1 - cos(x) = Sqr(3)*sin(x)
- Solution 1
- Since cos(0) = 1 and sin(0) = 0
- Hence LHS = 1 - 1 = 0
- Hence RHS = Sqr(3)*0 = 0
- Hence x = 0 is a solution and general solution is x = 2*n*pi
- Solution 2
- Since cos(120) = -1/2 and sin(120) = Sqr(3)/2
- Hence LHS = 1 - (-1/2) = 3/2
- Hence RHS = Sqr(3)*Sqr(3)/2 = 3/2
- Hence x = 120 is a solution and general solution is x = 2*n*pi + 2*pi/3
Go to Begin
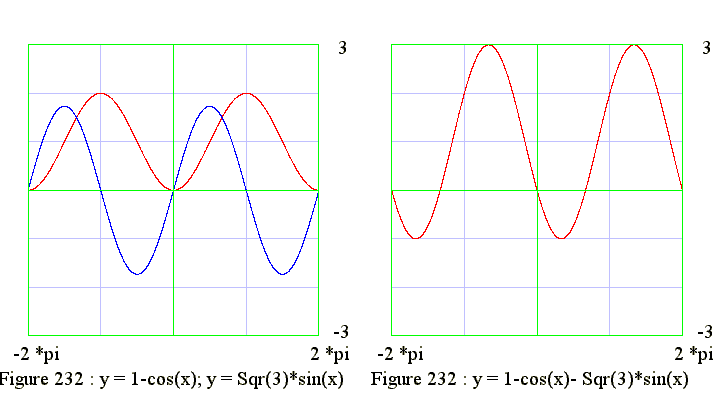
Q05. Graphic solution of two curves
Draw graphs of y = 1 - cos(x) and y = Sqr(3)*sin(x) in same scale
- From left side diagram we see that
- The intersections of the two curves at 0 and 120 degrees
- Hence x = 0 degrees and general solution is x = 2*n*pi
- Hence x = 120degrees and general solution is x = 28n*pi + 2*pi/3
Go to Begin
Q06. Graphic solution of one curves
Draw graph of y = 1 - cos(x) - Sqr(3)*sin(x)
- From right side diagram we see that
- The zeros of the curve are at 0 and 120 degrees
- Hence x = 0 degrees and general solution is x = 2*n*pi
- Hence x = 120degrees and general solution is x = 28n*pi + 2*pi/3
Go to Begin