Counter
Mathematics Dictionary
Dr. K. G. Shih
Figure 308 : Ellipse in rectangular form

  • Q01 | - Diagram : Ellipse in rectangular form
  • Q02 | - Find locus of 9*x^2 + 25*y^2 - 18*x + 50*y - 191 = 0
  • Q03 | - Find locus of 9*x^2 + 25*y^2 - 18*x + 50*y + 34 = 0
  • Q04 | - Find locus of 9*x^2 + 25*y^2 - 18*x + 50*y + 50 = 0
  • Q05 | - Parametric form
  • Q06 | - Reference

Q01. Diagram : Ellipse in rectangular form


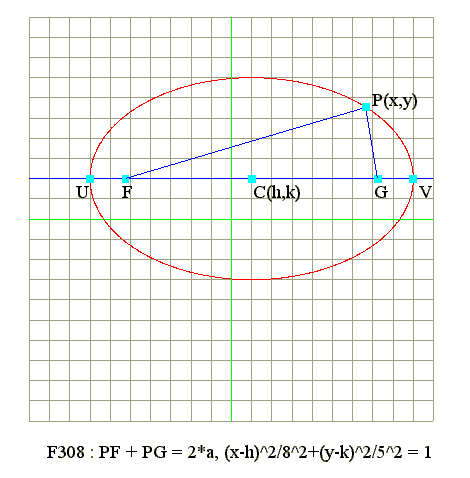
Go to Begin

Q02. Find locus of 9*x^2 + 25*y^2 - 18*x + 50*y - 191 = 0

Question
  • 1. Find seme-axese and focal length
  • 2. Find coordinates of coci and vertices
Solution
  • Use completing the square
  • 9*(x^2 - 2*x + 1 - 1) + 25*(y^2 + 2*y + 1 - 1) = 191
  • 9*(x - 1)^2 - 9 + 25*(y + 1)^2 - 25 = 191
  • 9*(x - 1)^2 + 25*(y + 1)^2 = 191 + 9 + 25
  • 9*(x - 1)^2 + 25*(y + 1)^2 = 225
  • ((x - 1)/5)^2 + ((y + 1)/3)^2 = 1
  • Hence semi-axese : a = 5 and b = 3
  • Focal length f = Sqr(a^2 - b^2) = 4
Find the coordinate of foci and vertices
  • Center (1, -1)
  • Focus F at (1 - 4, -1) or (-3, -1)
  • Focus G at (1 + 4, -1) or (+5, -1)
  • Vertex U at (1 - 5, -1) or (-4, -1)
  • Vertex V at (1 + 5, -1) or (+6, -1)

Go to Begin

Q03. Find locus of 9*x^2 + 25*y^2 - 18*x + 50*y + 34 = 0

Solution
  • Use completing square to convert it to standard form
  • 9*(x - 1)^2 + 25*(y + 1)^2 - 9 - 25 + 34 = 0
  • 9*(x - 1)^2 + 25*(y + 1)^2 = 0
  • Hence the locus is a point at (1, -1)

Go to Begin

Q04. Find locus of 9*x^2 + 25*y^2 - 9*x + 50*y + 50 = 0

Solution
  • Use completing square to convert it to standard form
  • 9*(x - 1)^2 + 25*(y + 1)^2 - 9 - 25 + 50 = 0
  • 9*(x - 1)^2 + 25*(y + 1)^2 = -16
  • Since the equation is not existed in real number system
  • Hence there is no locus in real number system

Go to Begin

Q05. Parametric form

Question
  • Prove that x = h + a*cos(t) and y = k + b*sin(t) is an ellipse
  • Since ((x - h)/a)^2 + ((y - k)/b)^2 = cos(t)^2 + sin(t)^2
  • We know that cos(t)^2 + sin(t)^2 = 1
  • Hence ((x - h)/a)^2 + ((y - k)/b)^2 = 1
  • This is an equation of ellipse

Go to Begin

Q06. Reference

Reference
Go to Begin
Show Room of MD2002 Contact Dr. Shih Math Examples Room
Copyright © Dr. K. G. Shih. Nova Scotia, Canada.
1