Counter
Mathematics Dictionary
Dr. K. G. Shih
Figure 311 : R = (D*e)/(1 + e*cos(A))

  • Q01 | - Diagram : R = (D*e)/(1 + e*cos(A))
  • Q02 | - Compare R = (D*e)/(1 + e*cos(A)) and R = (D*e)/(1 - e*cos(A))
  • Q03 | - Compare R = (D*e)/(1 + e*cos(A)) and R = (D*e)/(1 - e*sin(A))
  • Q04 | - Ellipse : R = (D*e)/(1 - e*cos(A))
  • Q05 | - Reference

Q01. Diagram : R = (D*e)/(1 + e*cos(A))


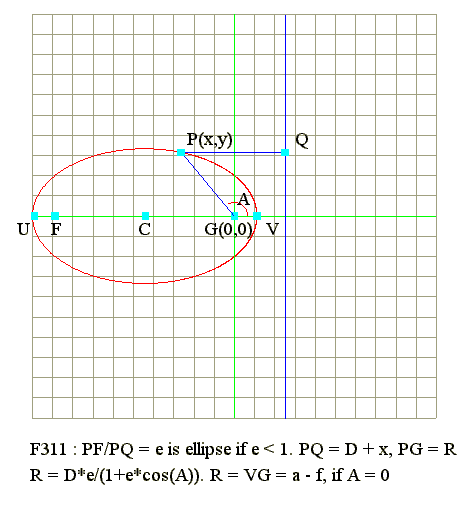
Go to Begin

Q02. Compare R = (D*e)/(1 + e*cos(A)) and R = (D*e)/(1 - e*cos(A))

R = (D*e)/(1 + e*cos(A))
  • Directrix is at right side of ellipse
  • Origin is at focus G(0, 0)
  • Center is at (-f, 0)
  • Rectangular form is ((x + f)/a)^2 + (y/b)^2 = 1
R = (D*e)/(1 - e*cos(A))
  • Directrix is at left side of ellipse
  • Origin is focus F(0, 0)
  • Center is at (f, 0)
  • Rectangular form is ((x - f)/a)^2 + (y/b)^2 = 1

Go to Begin

Q03. Compare R = (D*e)/(1 + e*cos(A)) and R = (D*e)/(1 - e*sin(A))

R = (D*e)/(1 + e*cos(A))
  • Directrix is at right side of ellipse
  • Origin is at focus G(0, 0)
  • Center is at (-f, 0)
  • Rectangular form is ((x + f)/a)^2 + (y/b)^2 = 1
R = (D*e)/(1 - e*sin(A))
  • Directrix is at top of ellipse
  • Origin is focus F(0, 0)
  • Center is at (0, -f,)
  • Rectangular form is (x/a)^2 + ((y + f)/b)^2 = 1
Diagram
Go to Begin

Q04. Ellipse : R = (D*e)/(1 - e*cos(A))

Ellipse in polar form
Go to Begin

Q05. Reference
Go to Begin
Show Room of MD2002 Contact Dr. Shih Math Examples Room
Copyright © Dr. K. G. Shih. Nova Scotia, Canada.
1