-
Q01 |
- Diagram to Solve x^5 - 1 = 0
- Q02 | - DeMovire's theory
- Q03 | - Solve x^5 - 1 = 0 by DeMovire's theory
- Q04 | - Solve x^5 - 1 = 0 by construction
- Q05 | - Solve x^4 + x^3 + x^2 + x + 1 = 0
- Q06 | - Reference
- Q02 | - DeMovire's theory
Q01. Diagram : Solve x^5 - 1 = 0
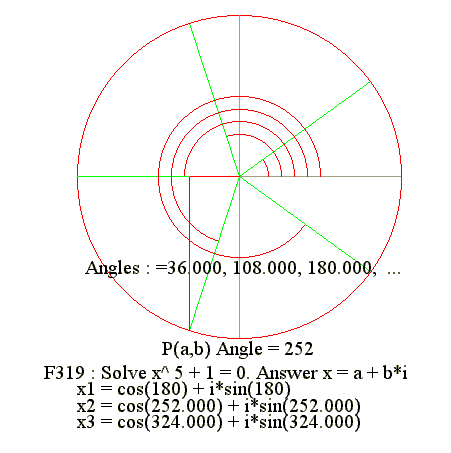
|
Go to Begin
Q02. DeMovire's thoery
Rule 1
- (cos(A) + i*sin(A))^n = cos(n*A) + i*sin(n*A)
- (cos(A) + i*sin(A))^(1/n) = cos((2*k*pi + A)/n) + i*sin((2*k*pi + A)/n)
- Where k = 0, 1, 2, .... (n - 1)
Go to Begin
Q03. Solve x^5 - 1 = 0 by DeMovire's theory
Change x^5 = 1 to polar form
- x^5 = cos(0) + i*sin(0)
- x = (cos(0) + i*sin(0))^(1/5)
- x = cos((2*k*pi + 0)/5) + i*sin((2*k*pi + 0)/5)
- k = 0, x0 = cos(000) + i*sin(000) = 1
- k = 1, x1 = cos(072) + i*sin(072)
- k = 2, x2 = cos(144) + i*sin(144)
- k = 3, x3 = cos(216) + i*sin(216)
- k = 4, x4 = cos(288) + i*sin(288)
- x0 and x4 are conjugate
- Sum of roots is real
- x1 + x4 = cos(72) + i*sin(72) + cos(288) + i*sin(288)
- = cos(72) + i*sin(72) + cos(360 - 72) + i*sin(360 - 72)
- = cos(72) + i*sin(72) + cos(72) - i*sin(72)
- = 2*cos(72)
- = Real number
- Product of root is real
- x1*x4 = (cos(72) + i*sin(72))*(cos(288) + i*sin(288))
- = (cos(72) + i*sin(72))*(cos(360 - 72) + i*sin(360 - 72))
- = (cos(72) + i*sin(72))*(cos(72) - i*sin(72))
- = cos(72)^2 - (i^2)*sin(72)^2
- = 1
- = real number
- x2 and x3 are conjugate
- Sum of roots is real
- x2 + x3 = cos(144) + i*sin(144) + cos(216) + i*sin(216)
- = cos(180 - 36) + i*sin(180 - 36) + cos(180 + 36) + i*sin(180 + 36)
- = -cos(36) + i*sin(36) - cos(36) - i*sin(36)
- = -2*cos(36)
- = Real number
- Product of root is real
- x2*x3 = (cos(144) + i*sin(144))*(cos(216) + i*sin(216))
- = (-cos(36) + i*sin(36))*(-cos(36) - i*sin(36))
- = cos(36)^2 - (i^2)*sin(36)^2
- = cos(36)^2 + sin(36)^2
- = 1
- = Real number
- x2*x3 = (cos(144) + i*sin(144))*(cos(216) + i*sin(216))
- = (-cos(36) + i*sin(36))*(-cos(36) - i*sin(36))
- = cos(36)^2 - (i^2)*sin(36)^2
- = cos(36)^2 + sin(36)^2
- = 1
- = Real number
- sin(180 - A) = +sin(A)
- sin(180 + A) = -sin(A)
- sin(360 - A) = -sin(A)
- cos(180 - A) = -cos(A)
- cos(180 + A) = -cos(A)
- cos(360 - A) = +cos(A)
Go to Begin
Q04. Solve x^5 - 1 = 0 by construction
Construction
- Draw a large unit circle (Radius = 1 unit)
- Draw five points P, Q, R, S, T on circle
- Draw angle A0 = angle POX = 000
- Draw angle A1 = angle QOX = 072
- Draw angle A2 = angle ROX = 144
- Draw angle A3 = angle SOX = 216
- Draw angle A4 = angle TOX = 288
- Find root r1
- Let coordinates Q be (x1, y1)
- Measure x0 and y0 then r1 = x1 + i*y1
- Find root r2
- Let coordinates R be (x2, y2)
- Measure x0 and y0 then r2 = x2 + i*y2
- r3 is conjugate of r2
- r4 is conjugate of r1
Go to Begin
Q05. Solve x^4 + x^3 + x^2 + x + 1 = 0
Use solution of x^5 - 1 = 0
- Since x^5 - 1 = (x - 1)*(x^4 + x^3 + x^2 + x + 1)
- The roots are r1, r2, r3, r4
- r1 = cos(072) + i*sin(072)
- r2 = cos(144) + i*sin(144)
- r3 = cos(216) + i*sin(216)
- r4 = cos(288) + i*sin(288)
Go to Begin
Q06. Reference
Go to Begin
