Figure 321 : Angle 30 and 45 degrees
Q01. Diagram : Angle 30 and angle 45
|
Go to Begin
Q02. Special value for angle is 30 degrees
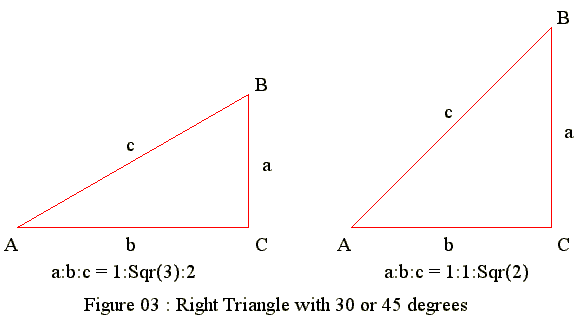
Let angle A = 30 and angle C = 90
- Geometric theory
- The opposite side of angle A is 1,
- The Hypothese is 2 (Geometric theory).
- Hence Adjacent of angle A is Sqr(2^2 - 1) = Sqr(3)
- The values of the ratios are
- sin(30) = Opp/Hyp = 1/2.
- cos(30) = Adj/Hyp = Sqr(3)/2.
- Tan(30) = Opp/Adj = 1/Sqr(3) = Sqr(3)/3.
- csc(30) = Hyp/Opp = 2.
- sec(30) = Hyp/Adj = 2/Sqr(3) = 2*Sqr(3)/3.
- cot(30) = Adj/Opp = Sqr(3).
Go to Begin
Q03. Special value for angle is 45 degrees
Let angle A = 45 and angle C = 90
- Geometric theory
- The opposite side of angle A is 1
- The adjacent side is also 1.
- Hence hypothese Sqr(1^2 + 1^2) = Sqr(2)
- The values of the ratios are
- sin(45) = Opp/Hyp = Sqr(2)/2.
- cos(45) = Adj/Hyp = Sqr(2)/2.
- Tan(45) = Opp/Adj = 1.
- csc(45) = Hyp/Opp = 2/Sqr(2) = Sqr(2).
- sec(45) = Hyp/Adj = 2/Sqr(2) = Sqr(2).
- cot(45) = Adj/Opp = 1.
Go to Begin
Q04. Special value for angle is 60 degrees
Let angle A = 60 and angle C = 90
- Geometric theory
- If hypothese is 2, then adjacent side of A is 1.
- Hence Oppsite side of angle A is Sqr(2^2 - 1) = Sqr(3)
- The values of the ratios are
- sin(60) = Opp/Hyp = Sqr(3)/2.
- cos(60) = Adj/Hyp = 1/2.
- Tan(60) = Opp/Adj = 1/Sqr(3) = Sqr(3)/3.
- csc(60) = Hyp/Opp = 2/Sqr(3) = 2*Sqr(3)/3..
- sec(60) = Hyp/Adj = 2.
- cot(60) = Adj/Opp = 1/Sqr(3) = Sqr(3)/3.
Go to Begin
Q05. Prove opposite side of angle 30 is half of hypothese
Construction
- Let mid point of AC is E
- Let mid point of AB is F
- Let angle BAC = 30 degrees
- EF parallel to BC (Mid point theory)
- Hence EF bisects AC
- Hence AF = FC
- Hence angle ECF = 30 dgrees
- Hence angle BCF = angle CFB = FBC
- Hence BC = BF = AB/2
Go to Begin