Mathematics Dictionary
Dr. K. G. Shih

    Figure 065 : Names of quarilaterals


  • Q01 | - Diagram : Names of quarilaterals
  • Q02 | - Properties of parallelogram
  • Q03 | - Square and rhombus
  • Q04 | - Recangle
  • Q05 | - Find area
  • Q06 | - Symmetrical axese of regular polygon

    Q01. Diagram


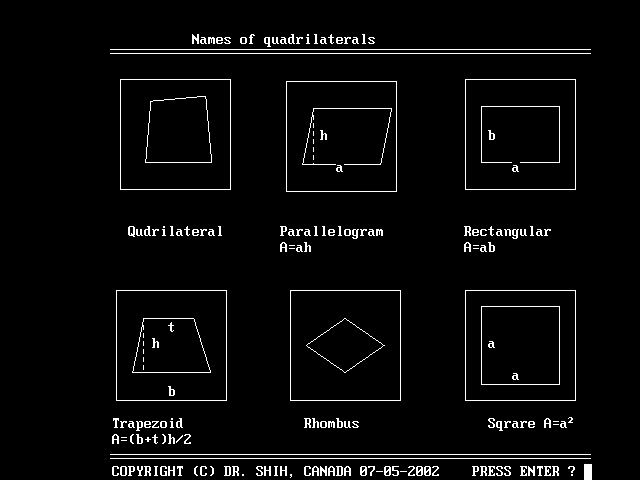
    Go to Begin

    Q02. Properties of parallelogram

    Parallelogram
    • 1. Opssosite sides are parallel
    • 2. Opssosite sides are parallel and equal
    • 3. Opposite angles are equal
    • 4. Diagonals bisect each other
    • 5. Two neighbour angles are supplemintary

    Go to Begin

    Q03. Square and rhombus

    Squre
    • 1. Four sides are equal
    • 2. Opssosite sides are parallel and equal
    • 3. Each internal angle = 90 degrees
    • 4. Diagonals bisect each other and perpendicular each other
    • 5. It has 4 symmetrical axis
      • Two Side to side perpendicular lines
      • Two Veterx to vertex lines
    Rhombus
    • 1. Four sides are equal
    • 2. Opssosite sides are parallel and equal
    • 3. Opposite angles are equal
    • 4. Each internal angle = 90 degrees
    • 5. Diagonals bisect each other but not perpendicular each other
    • 6. It has 2 symmetrical axis

    Go to Begin

    Q04. Rectangle

  • 1. Two opposite sides are equal
  • 2. Opssosite sides are parallel and equal
  • 3. Each internal angle = 90 degrees
  • 4. Diagonals bisect each other but not perpendicular each other
  • 5. It has 2 symmetrical axis
    Go to Begin

    Q05. Symmetrical axises of regular polygon

    Area of square
    • Let side be a
    • Area = a^2
    Area of rectangle
    • Let side be a and b
    • Area = a*b
    Area of rhombus : Use cosine law
    • Let side be a and one angle be U
    • Let diagonals be b and c
    • Use cosine law
      • b^2 = a^2 + a^2 - 2*a*a*cos(U) = 2*(a^2)*(1 - cos(U))
      • c^2 = a^2 + a^2 - 2*a*a*cos(pi - U) = = 2*(a^2)*(1 + cos(U))
    • Area
      • = b*c
      • = 2*(a^2)*Sqr((1 - cos(U))*(1 + cos(U)))
      • = 2*(a^2)*Sqr((1 - cos(U)^2))
      • = 2*(a^2)*Sqr(sin(U)^2)
      • = 2*(a^2)*sin(U)
    Area of rhombus : Use 4 right angle triangle
    • Let side be a and one angle be U
    • Right angle triangle
      • Hypothese = a
      • Angle 1 = U/2 and side1 = a*sin(U/2)
      • Angle 2 = (pi - U)/2 and side 2 = a*sin(pi/2 - U/2) = a*cos(U/2)
      • area = (side 1)*(side 2) = (a^2)*sin(U/2)*cos(U/2) = (a^2)*sin(U)/2
    • Area of rhombus = 4*(area of triangle) = 2*(a^2)*sin(U)
    Area of parallelogram
    • Let sides AB = u and AC = v
    • Height h = u*sin(BAC)
    • Area = h*v/2 = u*v*sin(A)/2

    Go to Begin

    Q06. Symmetrical axises of regular polygon

    Example 1 : Equal size triangle has 3 symmetrical axese
    • From vertex draw line perpendicular to the oppsite side
    • Hence we can draw 3 symmetrical axese
    Example 2 : Square has 4 symmetrical axese
    • Vertex to vertex
      • From vertex draw line perpendicular to the oppsite vertex
      • Hence we can draw 2 symmetrical axese
    • Side to side
      • From mid point of one side draw line to mid point of opposite side
      • Hence we can draw another 2 symmetrical axese
    • Square can have total 4 symmetrical axese
    Example 3
    • 1. Regular Pentagon has 5 symmetrical axese
    • 2. Regular Pentagon has 6 symmetrical axese
    Defintion of polygon
    • Regular polygons : Their sizes are equal.
    • Number of symmetrical axes of regular polygon equal to number of sides
    • Each internal angle is (n*pi - 2*pi)/n
    Examples
    • Equilateral triangle : Each angle = (3*pi - pi)/3 = 60 degrees
    • Square : Each angle = (4*pi - 2*pi)/4 = 90 degrees
    • Pentagon : Each angle = (5*pi - 2*pi)/5 = 108 degrees

    Go to Begin
    Show Room of MD2002 Contact Dr. Shih Math Examples Room
    Copyright © Dr. K. G. Shih. Nova Scotia, Canada.
    1