-
Q01 |
- Diagram : Golden rectangle
- Q02 | - Definition and constructioin
- Q03 | - Prove that (length/width) = (1 + Sqr(5))/2
- Q04 | - Golden ration
- Q05 | - Golden rectangle after removing a square
- Q06 | - Golden ratio equation : 1/x = x/(1 + x)
- Q02 | - Definition and constructioin
Q01. Diagram : Golden rectangle
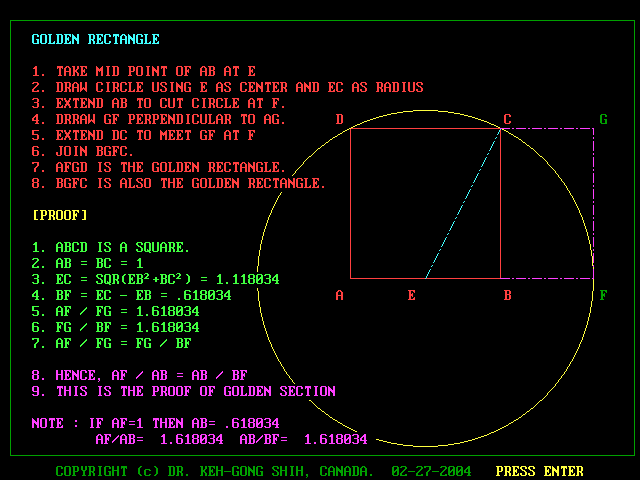
|
Go to Begin
Q02. Definition and constructioin
Definition
- Rectangle AFGD
- AF = length and GF = width
- (AF)/(FG) = (1 + Sqr(5))/2
- Draw a square ABCD
- Let E be the mid-point of AB
- Joint EC
- Draw a corcle with E as center and EC as radius
- Extend AB to meet circle at F
- Draw tangent at F and extend DC and meet tangent at G
- Rectangle AFGD is the golden rectangle
Go to Begin
Q03. Prove that (Length/width) = (1 + Sqr(5))/2
Proof
- (EC)^2 = ((EB)^2 + (BC)^2
- = (AB/2)^2 + (AB)^2
- = (AB)*(5/4)
- Hence EC = (Sqr(5)*AB)/2
- AF = EF + AE
- = EC + AB/2
- = Sqr(5)*AB/2 + AB/2
- = (AB)*(1 + Sqr(5))/2
- Since AB = EF
- Hence AF/EF = (1 + Sqr(5))/2 = 1.6180339887....
- This decimal value will go on forever without repeating
Go to Begin
Q04. Gorden ratio
Definition
- Draw a line AB and extend to C
- Let BC = 0.6180339887.....
- AC/AB = (1 + Sqr(5))/2 = 1.6180339887....
- This is called gorlden ratio
Go to Begin
Q05. Golden rectangle after removing a square
Definition
- Golden rectangle after removing square ABC
- We have rectangle BCGF
- BCGF is also golden rectangle
- FG/EF = AB/EF
- = 1/0.6180339887.....
- = 1.6180339887....
- Hence BCFG is gorlden ratio
Go to Begin
Q06. Golden ratio equation : 1/x = x/(1 + x)
- x^2 = x + 1
- x^2 - x - 1 = 0
- Hence x = (1 + Sqr(5))/2
Go to Begin
