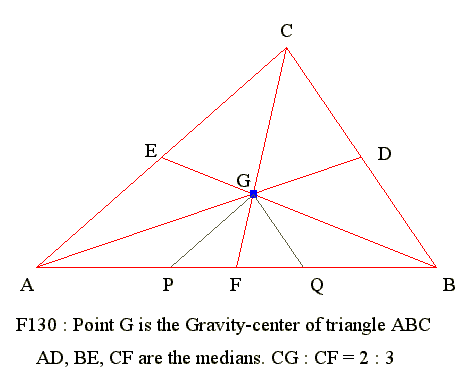
-
Symbol Defintion
Example x^2 = square of x
GE 03 01. Various names of triangle
Defintions
- Study | Names of triangles
- Start diagram program
- Write down the definitions of various triangles
- Each angle = 60 degrees
- The sides are all equal
Go to Begin
GE 03 02. Five centers of triangle
Defintions
- Study | Five centers of triangles
- Sketch triangle with in-center
- Sketch triangle with circum-center
- Sketch triangle with ex-center
- Sketch triangle with gravity-center
- Sketch triangle with ortho-center
Go to Begin
GE 03 03. Study five centers of triangle
Diagrams
- See GE 03 02
Go to Begin
GE 03 04. Pedal triangle
Diagram


- Three feet of altidudes of trangle ABC are at D, E, F
- Triangle DEF is called pedal triangle
- In-center of pedal triangle is coincided with the orthocenter of triangle ABC
- Construction method
- Geometric method
- Analytic method : See AN 11 08
Go to Begin
Q05. Ex-central triangle
Diagram


- Three ex-center triangle ABC are at J, K, L
- Triangle JKL is called ex-central triangle
- In-center of triangle ABC is coincided with the orthocenter of triangle JKL
- Construction method :
- Geometric method :
- Analytic method : See AN 11 09
Go to Begin
GE 03 06. Property of pedal triangle
Construction
- Draw triangle ABC
- Draw AD perpendicular to BC
- Draw BE perpendicular to CA
- Draw CF perpendicular to AB
- Join D,E,F to make a triangle which is pedal triangle
- ABDE are concyclic if AB as diameter
- BCEF are concyclic if BC as diameter
- CAFD are concyclic if CA as diameter
- Triangle CDE is similar to triangle ABC
- Triangle AEF is similar to triangle ABC
- Triangle BFD is similar to triangle ABC
- Geometric method :
- Analytic geometric method : See AN 11 08
Go to Begin
GE 03 07. Property of ex-central triangle
Construction
- Draw triangle ABC
- Draw ex-center J
- Draw ex-center K
- Draw ex-center L
- Join J,K,L as triangle which is ex-central triangle
- J, C, K are colinear
- K, A, L are colinear
- L, B, J are colinear
- In-center of triangle ABC is coincided with ortho-center of triangle JKL
- Geometric method :
- Analytic geometric method : See AN 11 08
Go to Begin
GE 03 08. Ortho-center and circum-center of triangle ABC
Diagram
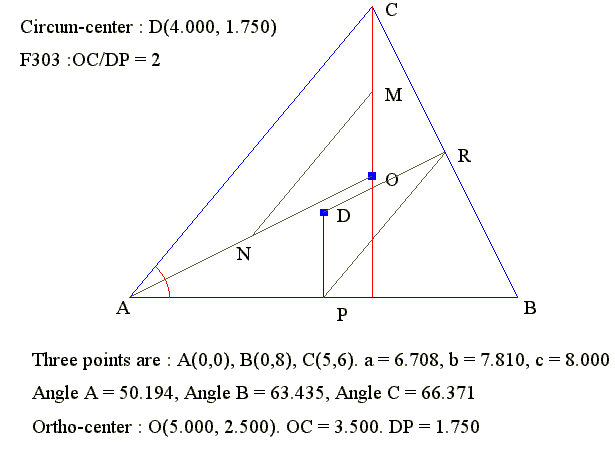
- Draw a large triangle ABC
- Draw the ortho-center O
- Draw the circum-center D
- Let COH be perpendicular AB
- Let DP be the bisector of AB
- CO : DP = 2 : 1
- Geometric method :
- Analytic geometric method : See AN 11 11
Go to Begin
GE 03 09. Ortho-center, centroid and circum-center are colinear
Diagram

- Draw a large tiangle ABC
- Draw ortho-center O
- Draw centroid G
- Draw circum-center Q
- O, G and Q are colinear
- Geometric method :
- Analytic geometric method : See AN 11 10
Go to Begin
GE 03 10. Locus about five centers of triangle
Diagrams
- Study | Section 10 : Locus
- Trangle ABC : A and B are fixed points. Angle ACB moving with ACB as constnat
- Theory : Point C is always on arc ACB
- The circle is called circum-circle
- Locus of in-center of triangle ABC
- Locus of ex-center of triangle ABC
- Locus of centroid of triangle ABC
Go to Begin
GE 03 11. Give three sides to draw a triangle
Construction
- Draw one side using line 1 as AB
- Use one end A of line 1 as center and line 2 as radius draw a circle
- Use other end B of line 1 as center and line 3 as radius draw a circle
- Two circles intersect at C
- Join AC and BC
- ABC is the required triangle
Go to Begin
GE 03 12. Use three given heights of triangle to draw a triangle
Construction
- Let h1 be perpendicular to BC which is a
- Let h2 be perpendicular to CA which is b
- Let h3 be perpendicular to AB which is c
- Using area of triangle we have a*h1 = b*h2 = c*h3 = r
- Let r = h1*h2*h3
- Hence a = h2*h3, b = h3*h1 and c = h1*h2
- Since 3 sides are known, hence we can draw a triangle UVW
- Draw trinagle ABC with given heights
- Draw the heights of triangle UVW
- Along height from U, from VW to draw line to point A and equal h1
- Draw line from A to parallel to UV and meets line UV at B
- Draw line from A to parallel to VW and meets line UV at C
- ABC is the required triangle
- Triangle ABC is similar to UVW
- From area triangle UVW we have u*p1 = v*p2 = w*p3
- The heights of ABC equal the given height h1,h2,h3
Go to Begin
GE 03 13. Use three given medians of triangle to draw a triangle
Diagram
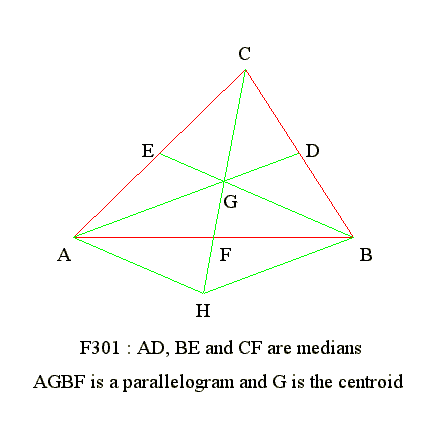
Construction
- Draw triangle BGH and G is the centroid
- HG = 2*AD/3 and AD is median
- BG = 2*BE/3 and BE is median
- BH = 2*CF/3 and CF is median
- Produce HG to A and AG = HG
- Join A and B
- Draw GC parallel and equal to BH.
- ABC is the required trinagle
- Since BGCH is parallelogram
- Hence BC and GH bisect each orhter at D.
- D is mid point of BC
- AD is one given median
- Draw CG and meet AB at F
- In triangle ABH, GF parallel to BH
- Since G is mid-point of AH, Hence F is mid-point of AB
- By centroid theory, CF is median and equal the given median
- Draw BG and meet AC at E
- In triangle ACH, GE parallel to CH
- Since G is mid-point of AH, Hence E is mid-point of AC
- By centroid theory, BC is median and equal the given median
- Similarly, we can prove that CF is median and F is mid point of AB
- Hence ABC is the required triangle
Go to Begin
GE 03 14. Triangle ABC and Median CF : AC^2 + BC^2 = 2*(CF^2) + (AB^2)/2
Question
- Triangle ABC and CF is median
- Prove that AC^2 + BC^2 = 2*(CM^2) + (AB^2)/2
- Produce AB to Q and let CQ perpendicular to AQ
- Let F be mid-point of AB and CF is the median
- Let BQ = x and CQ = y
- Triangle CBQ
- BC^2 = x^2 + y^2
- Triangle CFQ
- CF^2 = (AB/2 + x)^2 + y^2 = AB^2/4 + AB*x + x^2 + y^2
- Triangle CAQ
- CA^2 = (AB + x)^2 + y^2 = AB^2 + 2*AB*x + x^2 + y^2
- LHS
- AC^2 + BC^2 = AB^2 + 2*AB*x + 2*x^2 + 2*y^2
- RHS
- 2*(CM^2) + (AB^2)/2
- = (AB^2)/2 + 2*AB*x + 2*x^2 + 2*y^2 + (AB^2)/2
- = AB^2 + 2*AB*x + 2*x^2 + 2*y^2
- Hence AC^2 + BC^2 = 2*(CM^2) + (AB^2)/2
- Let angles CAB and CBA be both acute angle
- Prove that AC^2 + BC^2 = 2*(CM^2) + (AB^2)/2
Go to Begin
GE 03 00. Outlines
Theory
- Ortho-center, centroid and circum-center of triangle ABC are colinear
- Relation of Ortho-center and circum-center of triangle ABC
- Property of ex-central triangle
- Property of pedal triangle
- Theory of in-center of triangle
- Theory of ex-center of triangle
- Theory of circum-center of triangle
- Theory of centroid of triangle
- Theory of ortho-center of triangle
- Locus of in-center of triangle ABC
- Locus of ex-center of triangle ABC
- Locus of centroid of triangle ABC
- Find the names
- 1. Give 3 sides
- 2. Give 3 medians
- 3. Give 3 heights
Go to Begin