-
Symbol Defintion
Sqr(x) = Square root of x
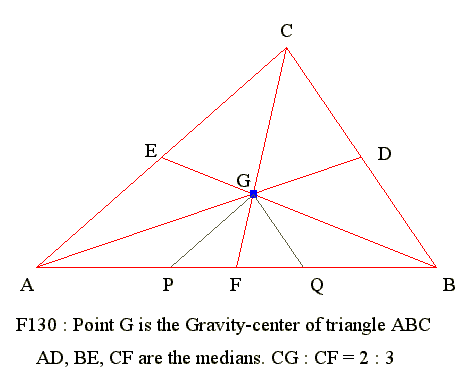
GE 14 01. What is centroid
Definition
- Medians of triangle are concurrent at a point G which is called centroid
- Centroid is also called gravity center of a triangle
- Three lines meet at one point is called concurrent
- Vertex of triangle to mid point of opposite side is called median
- AD, BE, CF are medians of triangle as shown in diagram
Go to Begin
GE 14 02. Medians of triangle are concurrent
diagram
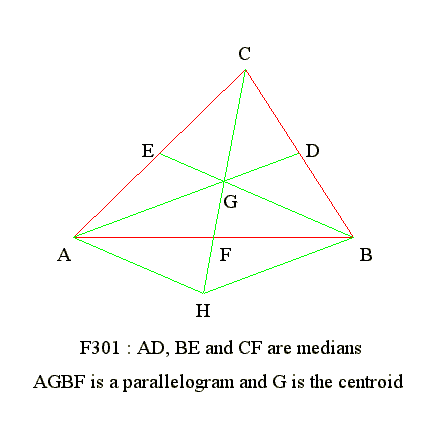
- Draw triangle ABC
- Let D be mid point of BC, E be midpoint of CA
- Draw medians AD and BE intersecting at G
- Join C and G. Produce CG to F on AB
- Produce CF to H and let FH = CG
- We want to prove that F is mid point of AB
- In triangle CAH E and G are mid points of CA and CH
- Hence EG parallel to AH (mid point theory)
- In triangle CBH D and G are mid points of BC and CH
- Hence DG parallel to BH
- Hence AGBH is a parallelogram (opposite sides parallel)
- Hence AF = BF (properties of parallelogram)
- Hence F is mid point and CF is medain passing G
Go to Begin
GE 14 03. Centroid to vertex is 2/3 of median
- In Q02, FH = FG (properties of parallelogram)
- Hence FG = GH/2 = CG/2
- CF = CG + FG = CG + CG/2 = 3*CG/2
- Or CG = 2*CG/3 where CG is the median
Go to Begin
Q04. Locus of centroid
diagram

- Let A and B are fixed and C is moving with angle ACB = constant
- Find locus of centroid
-
Diagram of geometry
Program 10 03
- Draw GP parallel to CA and P on AB
- Draw GQ parallel to BC and Q on AB
- Hence angle PGQ = angle ACB (fixed)
- Since GP parallel to CA hence AP = 2*AF/3
- Since GQ parallel to BC hence BQ = 2*BF/3
- AB is fixed and then AF and BF are fixed
- Hence P and Q are fixed points.
- Also PGQ is fixed angle.
- Hence locus of G is an arc of circle passing P, G, Q.
Go to Begin
GE 14 05. Coordinate geometry Prove that medians of triangle concurrent
Reference
-
Coordinate geometry
Program 11 05
Go to Begin
GE 14 06. Construct triangle if 3 medians are given
- See GE 03 12
Go to Begin
GE 14 07. Answer
Go to Begin
GE 14 08. Answer
Go to Begin
GE 14 09. Answer
Go to Begin
GE 14 10. Answer
Go to Begin
GE 14 00. Outline
- Centroid : medians are concurrent
- Two third rule : Centroid to vertex is 2/3 of it median
Go to Begin
