-
Symbol Defintion
Example : GT means greater than
GE 16 01. Ortho-center
Defintion
- Three heights of triangle are concurrent at a poin O which is ortho-center
- Draw a triangle ABC
- Draw height AD perpendicualar to BC
- Draw height BE perpendicualar to CA
- Draw height CF perpendicualar to AB
- Three height meets at one point O which is the orthocenter
Go to Begin
GE 16 02. Prove that three heights meet at one point
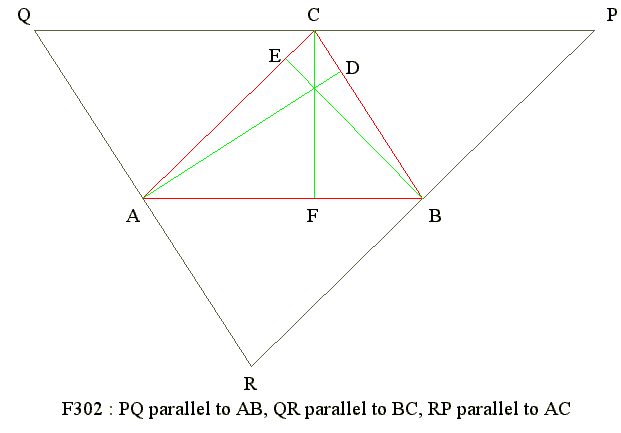
- Draw a large triangle ABC
- Draw AD perpendicular to BC
- Draw BE perpendicular to CA
- Draw CF perpendicular to AB
- Draw line parallel to AB and pass C
- Draw line parallel to BC and pass A
- Draw line parallel to CA and pass B
- Three parallel lines meet at P, Q, R
- P, C, Q are colinear
- Q, A, R are colinear
- R, B, P are colinear
- Hence PQR is a triangle
- CQ parallel to AB (construction)
- AQ parallel to BC (construction)
- Hence ABCQ is a parallelogram
- Hence QC = AB
- Similarly ABPC is a parallelogram
- Hence PC = AB
- Since CF perpendicular to AB and PQ parallel to AB
- Hence PC = QC and CF perpendiculer to PQ
- Hence CF bisects PQ
- Same as above
- Same as above
- Since CF, AD and BE are are bisectors of PQR
- Hence CF, AD and BE are concurrent at O (circum-center)
- But AD, BE nad CF are heigths of triangle ABC
- Hence heights of triangle are concurrent
Go to Begin
GE 16 03. Property 1 : Points A, B, P, Q are concylic
Construction
- Draw a large triangle
- Draw AP perpendicular to BC
- Draw BQ perpendicular to CA
- Draw CR perpendicular to AB
- Hence three feets of the heights are P, Q, R
- Angle APB = 90 degrees
- Angle AQB = 90 degrees
- Hence points A, B, P, Q are concylic if AB as diameter to draw a circle
- Similarly, B, C, Q, R are concylic if BC as diameter
- Similarly, C, A, R, P are concylic if BC as diameter
Go to Begin
Q04. Pedal triangle : the feets of the heights form a triangle
Construction
- Draw a large triangle
- Draw AP perpendicular to BC
- Draw BQ perpendicular to CA
- Draw CR perpendicular to AB
- Hence three feets of the heights are P, Q, R
- Pedal triangle contains four similar triangle
- Triangle APQ is similar as ABC
- Angle CQP + angle AQP = 180 degrees (supplementary)
- Angle AQP + angle ABC = 180 degrees (concyclic)
- Hence angle CQP = angle ABC
- Angle C is in common for these two triangle
- Hence they are similar
- Similarly, triangle AQR is similar to triangle ABC
- Similarly, triangle AQR is similar to triangle ABC
Go to Begin
GE 16 05. Ortho-center O of traingle ABC is also incenter of triangle PQR
Prove point O is in-center of triangle PQR
- BQ is bisector of angle PQR
- Triangle CQP is similar triangle AQR
- Hence angle AQR = angle CQP
- Angle AQR + RQB = 90
- Angle BQP + PQC = 90
- Hence BQR = BQP
- Hence BQ is bisector of angle PQR
- Similarly, AP is besector of angle QPR
- Similarly, CR is besector of angle PRQ
- Hence O is in-center of PQR
Go to Begin
GE 16 06. Ortho-center : relation with circum-center
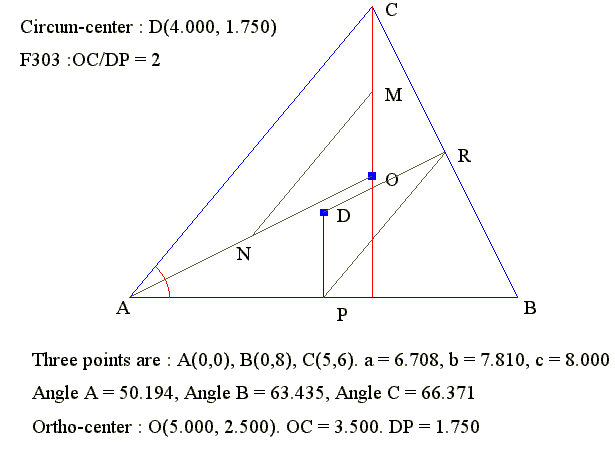
- Draw a large triangle
- Draw orthod-center O
- Draw circum-center D
- Draw COF perpendicular to AB
- Draw DP Perpendicular to AB as bisector
- Join mid point M of CO and mid point N of AO
- In triangle AOC we have MN = AC/2 and MN parallel to AC
- Join mid point R of BC and mid point P of AB
- In triangle ABC we have PR = AC/2 and PR parallel to AC
- Hence we can prove that triangle MON is similar to QOR
- PR parallel to MN
- DP parallel to MO
- NO parallel to DR
- Hence DP = MO = CO/2
- Hence CO : DP = 2 : 1
Go to Begin
GE 16 07. Angles of pedal triangle PQR and angles of triangle ABC
Angles of triangle PQR and angles of triangle ABC
- Angle PQR = 180 - 2*B
- Angle QRP = 180 - 2*C
- Angle RPQ = 180 - 2*A
- Since angle CQP = angle ABC and angle AQR = angle ABC
- Angle PQR = 180 - angle CQP - angle AQR
- Angle PQR = 180 - 2*angle ABC
- Similarly we prove other two cases
Go to Begin
GE 16 08. Sides of pedal triangle
Reference
- See GE 17 06
Go to Begin
GE 16 09. Distance between ortho-center and circum-center of triangle ABC
Formula
- The distance = R^2 - 8*(R^2)*cos(A)*cos(B)*cos(C)
- Reference : AN 11 09
Go to Begin
GE 16 10. Ortho-center to vertices of trinagle
Formula
- Ortho-center O
- OA = 2*R*cos(A)
- OB = 2*R*cos(B)
- OC = 2*R*cos(C)
- Reference : AN 11 10
Go to Begin
GE 16 11. Ortho-center to sides of triangle
- Ortho-center O. The feet of altitudes are P,Q,R
- OP = 2*R*cos(B)*cos(C) to side BC
- OQ = 2*R*cos(C)*cos(A) to side CA
- OR = 2*R*cos(A)*cos(B) to side AB
- Reference : AN 11 10
Go to Begin
GE 16 12. Ortho-center, centroid and circum-center are colinear

- Draw Ortho-center O
- Draw centoid G
- Draw circum-center V
- Diagram
-
Diagram
GE 21 09 : diagram 09 03
-
Diagram
GE 21 09 : diagram 09 03
Proof
- Join O,G,V
- Let M be mid-point of GO and N be mid-point of CG
- Hence MN = CO/2 and MN parallel to CO
- Also VF = CO/2 (GE 16 06)
- Angle MCN = angle GFV
- Hence triangle MGN and GVF are congruent (SAS)
- AGF is stri=aight line and angle FGV = angle MGN
- Hence O,G, V are colinear
- Verify by construction to show O, G, V are colinear
Go to Begin
GE 16 13. draw triangle if 3 medians are given
- See GE 03 11
Go to Begin
GE 16 14. References
Go to Begin
GE 16 00. Outline
- Ortho-center : The altitudes meet at one point
- Pedal trainalge : The feet of altitudes form a triangle
- Relation of ortho-center and circum-center
- Ortho-center of triangle ABC is the in-center of pedal triangle
Go to Begin
