Welcome to Mathematics Dictionary
Equilateral triangle - DP + DQ + DS = h

    Figure 118 : Equilateral triangle - DP + DQ + DS = h


  • Q01 | - Diagram
  • Q02 | - Equilateral triangle : DP + DQ + DS = height
  • Q03 | - Questions
  • Q04 | - Reference

    Q01. Diagram


    Equilateral triangle - Point D inside triangle DP + DQ + DS = h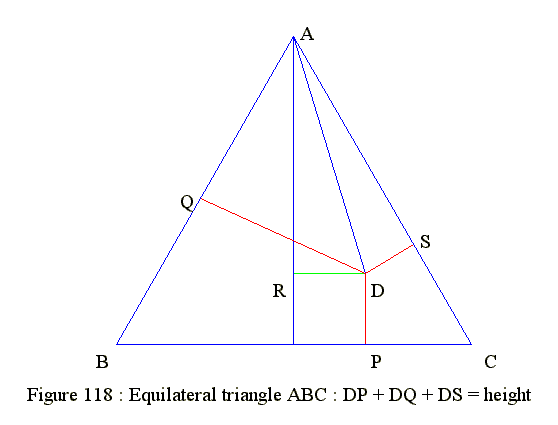


    Go to Begin

    Q2. Equilateral triangle : DP + DQ + DS = height

    Keywords
    • Equilateral triangle properties
    • sin(A) + sin(B) = 2*sin((A + B)/2)*cos((A - B)/2)
    Construction
    • 1. Draw an equilateral triangle
    • 2. Point D is inside triangle
    • 3. Draw DP, DQ and DS perpendicular to the sides
    • 4. Prove that DP + DQ + DS = h
    Proof
    • Angle BAD = 30 + angle RAD and Angle DAQ = 30 - angle RAD
    • Right triangle ADQ : DQ = AD*sin(30 - RAD)
    • Right triangle SAD : DS = AD*sin(30 + RAD)
    • Hence DQ + DS = AD*(sin(30 - RAD) + sin(30 + RAD))
    • Since sin(A) + sin(B) = 2*(sin((A+B)/2)*(cos(A-B)/2)
    • Hence DQ + DS = 2*AD*(sin(30)*cos(RAD))
    • = AD*cos(RAD)
    • = AR
    • Height = AR + DP = DP + DQ + DS

    Go to Begin

    Q03. Questions

    • 1. What is equilateral triangle ?
    • 2. What is the height of a triangle ?
    • 3. What is the distance from a point to the side of triangle ?
    • 4. What is formula of the sum of two functions in trigonometry ?

    Go to Begin

    Q04. Reference

    • Trigonometry TR 07 08 : Sum of two functions
    • Example : sin(A) + sin(B) = 2*(sin((A+B)/2)*(cos(A-B)/2)

    Go to Begin
    • Show Room of MD2002 Contact Dr. Shih Math Examples Room
    Copyright © Dr. K. G. Shih. Nova Scotia, Canada.
    1