Centroid
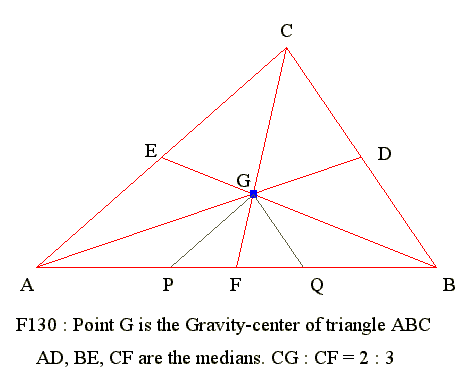

Q1. Centroid
Construction
- Draw a triangle ABC
- draw median AD to BC
- Draw median BE to CA
- Draw median CF to AB
- Intersection of medians G is the centroid or gravity center
Q2. Prove medians of triangle are concurrent
Proof
- Draw medians AD and BE
- Draw CG and extend to H
- Prove that F is mid-point of AB
- Triangle AHC
- Since G and E are mid-points
- Hence AH parallel to BE
- Triangle BHC
- Since G and D are mid-points
- Hence BH parallel to AC
- Hence AGBH is a parallelogram
- Hence AB and GH bisect each other
- Hence F is mid point of AB
- Hence CF is also a median
Q3. 2/3 rule Rule
- G is the centroid
- CF is the median
- Then CG = 2*CF/3
- From Q2, we know that GF = FH
- CG = GH = 2*GF
- CF = CG + GF = 3*GF
- Hence GF = CF/3
- Hence CG = 2*CF/3
Q4. Locus of centoid Question
- Triangle ABC
- verticce A and B are fixed
- If C moves with constant angle ACB
- Find the locus of centroid G
- Draw GP parallel to AC
- Draw GQ parallel to BC
- Hence angle PGQ = anglr ACB = fixed angle
- Also P and Q are fixed
- Hence P, G, Q are on arc of a circle