Mid point theory of triangle
Q01. Diagram
|
Go to Begin
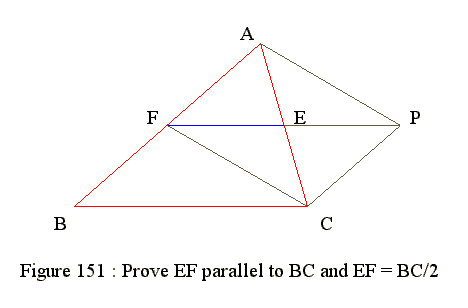
Q02. Prove that join mid points E, F of two sides and EF is parallel BC
Construct the triangle
- Draw triangle ABC
- Draw mid point E on AC
- Draw mid point F on AB
- Produce EF to EP and EP = EF
- Join AP and CP
Prove that AFCP is parallelogram
- Since AE = EC and EF = EP
- Hence AFCP is parallelogram
- Hence PC = AF = BF and BF parallel to PC
- Hence PCBF is parallelo gram
- Hence EF is parallel to BC
Go to Begin
Q03. Prove that join mid points E, F of two sides and EF = BC/2
Proof
- From above question we know PCBF is a pallelogram
- Hence FP = BC
- EP = 2*EF
- Hence EF = BC/2
Go to Begin
Q04. Join mid points of four sides of quadralateral and form a parallelogram
Proof
- Quadralateral ABCD
- Draw mid points E, F, G, H
- Join AC
- Triangle ACD
- FG parallel to AC and FG = AC/2
- Triangle ACB
- HE parallel to AC and HE = AC/2
- Hence EF parallel to HE and EF = HE
- Hence EFGH is parallelogram
Go to Begin
Q05. Prove that sin(30) = 1/2
Construction
- Let triangle ABC be right triangle
- Angle C = 90 degrees
- Angle A = 30 degrees
- Draw EF parallel to BC. E and F are mid points
- Then triangle EBC is equalateral triangle
- Hence BC = AB/2
- Triangle ABC : C = 90 degrees
- A = 30 degrees
- sin(A) = BC/AB
- Since AB = BC/2
- Hence sin(30) = 1/2
Go to Begin