Welcome to Mathematics Dictionary
Figure 221 : e^x + e^(2*x) + e^y + e^(2*y) = 12

    e^x + e^(2*x) + e^y + e^(2*y) = 12


  • Q01 | - Diagram
  • Q02 | - e^x + e^(2*x) + e^y + e^(2*y) = 12
  • Q03 | -
  • Q04 | -
  • Q05 | -

    Q01. Diagram of e^x + e^(2*x) + e^y + e^(2*y) = 12


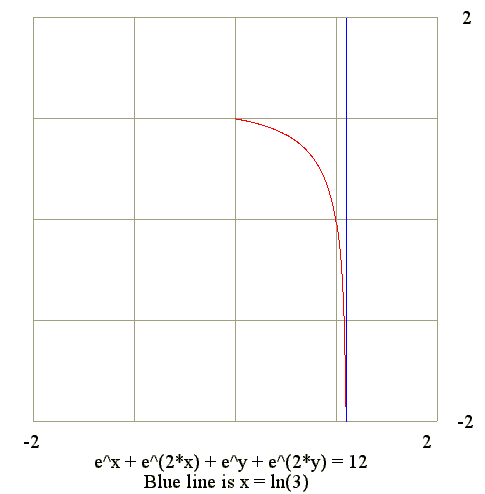
    Go to Begin

    Q02. e^x + e^(2*x) + e^y + e^(2*y) = 12

     Question : How to sketch the curve
    • 1. Change equation as y = f(x)
    • 2. (e^y)^2 + e^y + (e^x + e^(2*x) - 12) = 0
    • 3. Use quadratic formula to find e^y
    • 4. Hence we can have y = f(x)
    Question : How to find asymoptote of the curve
    • 1. when x = ln(3)
      • e^(x) = e^(ln(3)) = 3
      • e^(2*x) = (e^x)^2 = 9
    • 2. Hence we have e^y + e^(2*y) = 0
    • 3. But e^y = 0 means y = -infinite
    • 4. Hence asymptote is at x = ln(3)

    Go to Begin
    • Show Room of MD2002 Contact Dr. Shih Math Examples Room
    Copyright © Dr. K. G. Shih. Nova Scotia, Canada.
    1