Inverse of y = x^2 - 6*x + 8
Q01. Diagram : Inverse of y = x^2 - 6*x + 8
|
Go to Begin
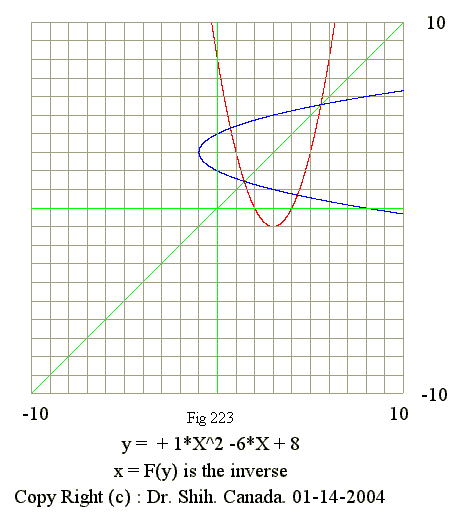
Q02. Inverse of y = x^2 - 6*x + 8
Intersection of y = x^2 - 6*x + 8 with inverse
- Estimate the points of intersection
- Inverse of y = x^2 - 6*x + 8
Go to Begin
Q03. Inverse of y = x^2 - 5*x + 8
Intersection of y = x^2 - 5*x + 8 with inverse
- Estimate the points of intersection
- Inverse of y = x^2 - 5*x + 8
Go to Begin
Q04. Quadratic function with inverse has one or none intersection
1. Intersection of y = x^2 - 2*x + 4 with inverse
- Estimate the points of intersection
- Diagram Inverse of y = x^2 - 2*x + 4
- Estimate the points of intersection
- Diagram Inverse of y = x^2 - 3*x + 4
Go to Begin
Q05. Discussion
Graphic solution
- The graphic solution is clear determine the signs of y, y' and y"
- The maximum and minimum points can only be estimated
-
Sketch program 06 10
- Procedures
- Open the program
- Click start
- Click 06 in upper box
- Click 10 in lower box
- Give coefficients : e.g. 1, -3, 4
- Procedures
- Find intersection with y = x first
- Hence we have x = a*x^2 + b*x + c
- If (b - 1)^2 - 4*a*c < 0, then no intersection
- If (b - 1)^2 - 4*a*c = 0, then one intersection
- If (b - 1)^2 - 4*a*c > 0, then two intersections or 4 intersections
Go to Begin