Counter
Mathematics Dictionary
Dr. K. G. Shih
Question and Answer
Questions



  • Subject | F308 - Equation of ellipse a*x^2 + c*y^2 + d*x + e*y + f = 0
    • Find locus of 9*x^2 + 25*y^2 - 18*x + 50*y - 191 = 0
    • Find locus of 9*x^2 + 25*y^2 - 18*x + 50*y + 34 = 0
    • Find locus of 9*x^2 + 25*y^2 - 18*x + 50*y + 50 = 0
  • Subject | F309 - Ellipse : Convert (x/a)^2 + (y/b)^2 = 1 to polar form
    • Find equation of directrix of (x/5)^2 + (y/3)^2 = 1
    • Convert (x/5)^2 + (y/3)^2 = 1 to polar form
  • Subject | F310 - Ellipse : Polar form
    • Convert R = (D*e)/(1 - e*cos(A)) to rectangular form
    • Convert R = 1.8/(1 - 0.8*cos(A)) to rectangular form
  • Keyword | S36 - Ellipse : Construct using locus definition
  • Keyword | Z002 - Equation : x^4 + x^3 + x^2 + x + 1 = 0
    • Find roots of x^5 - 1 = 0 first
    • Then use x^5 - 1 = (x - 1)*(x^4 + x^3 + x^2 + x + 1) to get solution
  • Keyword | S16 - Equation : x^5 - 1 = 0
  • Keyword | S86 - Equation : x^5 + 1 = 0
  • Keyword | S96 - Equation : x^4 - i = 0
  • Keyword | S97 - Equation : x^4 - i = 0
  • Keyword | S15 - Equation : x^7+ 2*x^6- 5*x^5- 13*x^4- 13*x^3- 5*x^2+ 2*x+ 1 = 0
  • Keyword | S106- Equilateral triangle : Circle inscribed triangle
  • Keyword | S112- Equilateral triangle : Distance of inside point to sides = height
  • Keyword | S35 - Equilateral triangle : Divide one side into 3 equal parts
  • Keyword | S113- Equilateral triangle : Divide one side into 3 equal parts
    Diagram for S113


  • Keyword | S106- Equilateral triangle : Circle inscribed triangle
  • Keyword | S81 - Equilateral triangle : Inscribed unit circle : PA^2 + PB^2 + PC^2 = 2*3
  • Keyword | S107- Equilateral triangle : Square inscribed triangle
  • Keyword | S39 - Equilateral triangle : Sum of distance of inside point D to sides
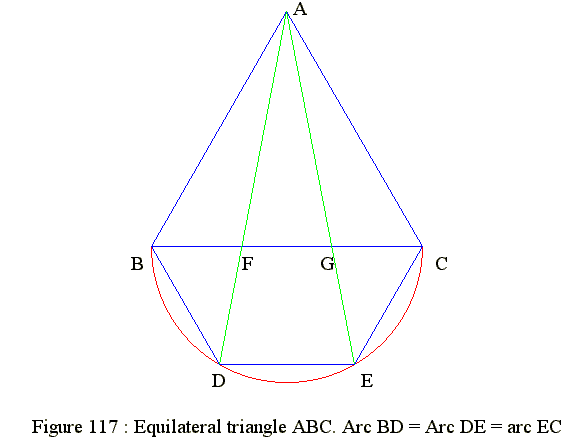
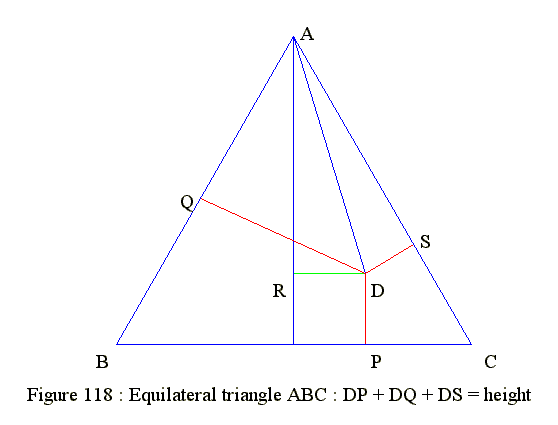
    Diagram for S39



  • Keyword | F221- Exponent : Example for e^x + e^(2*x) + e^y + e^(2*y) = 12
    • 1. How to ketch the curve ?
    • 2. Find the asymptote
  • Keyword | Z003- Ex-central triangle : Definition and construction
    • 1. Construct ex-central triangle
    • 2. Construct pedal triangle
  • Keyword | S23 - Ex-central triangle

    Go to Begin
    • Show Room of MD2002 Contact Dr. Shih Math Examples Room
    Copyright © Dr. K. G. Shih, Nova Scotia, Canada.
    1