Mathematics Dictionary Dr. K. G. Shih

---

Examples in geometry

Questions

Symbol Defintion Sqr(x) = Square root of x

GE 27 01 | - Triangle : Construct triangle if b,c and median AD = m1 are given GE 27 02 | - Triangle ABC : median AD = m1, medina BE = m2 and c are given GE 27 03 | - Circle : Three corcles touch each other with common tangent GE 27 04 | - Square with 4 semi-circles GE 27 05 | - Circle inscribed an equilateral triangle GE 27 06 | - Circle inscribed an equilateral triangle GE 27 07 | - Square inscribed an equilateral triangle GE 27 08 | - Triangle : Area of triangle formed by medians GE 27 09 | - Equilateral triangle : Medians and heights GE 27 10 | - Petal triangle of an equilateral triangle GE 27 11 | - Ex-central triangle of an equilateral triangle GE 27 12 | - Pedal triangle of triangle GE 27 13 | - Ex-central triangle of triangle GE 27 14 | - Triangle : Divide triangle into 4 congruent triangles GE 27 15 | - Ortho-center, centroid and circum-center of triangle are colinear GE 27 16 | - Prove cos(A-B) = cos(A)*cos(B) + sin(A)*sin(B) GE 27 17 | - Equilateral triangle : Divide side into three equal parts GE 27 18 | - Euilateral triangle : Sum of inside point to sides equals height GE 27 19 | - Three points with one point varying on y-axis GE 27 20 | - Equilateral triangle : regular hexagon inscribed triangle GE 27 21 | - Heights of triangle ABC are concurrent

Answers

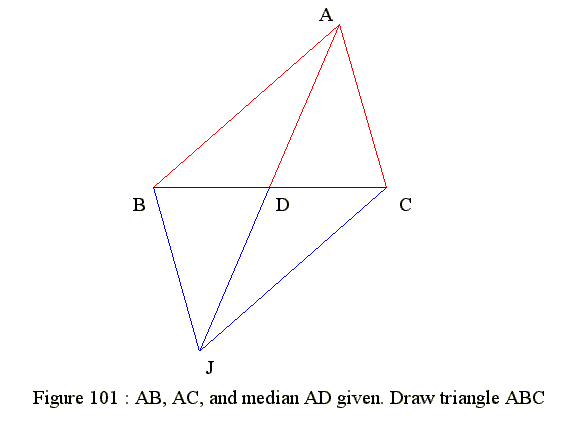
GE 27 01. Construct triangle if b,c and median AD are given Given Triangle ABC : AB = c = 10, CA = b = 6 and median AD = m1 = 7 Construct triangle ABC Construction Draw triangle ACJ AC = b, CJ = c and AJ = 2*m1 Since 3 sides are known hence we can draw triangle ACJ Let D be mid point of AJ Join CD and produce CD to B. Let BD = DC Join AB and triangle ABC is the required angle Proof Since BC and AJ bisect each other, hence ACBJ is a parallelogram Then AB = CJ = c AC = b by construction AD = AJ/2 = m1 by construction Hence triangle ABC is the required triangle Diagram Go to Begin GE 27 02. Triangle ABC : median AD = m1, medina BE = m2 and AB = c are given Given Median AD = 14, BE = 27 and c = 27 Construct triangle ABC Construction Let G be the gravity center of triangle ABC Let AG = 2*m1/3, BG = 2*m2/3 and AB = c Then 3 sides of triangle ABG are known, hence we can construct ABG Produce BG to E and let EG = BG/2 Produce AG to D and let GD = AG/2 Line AE and line BD meet a point C Triangle ABC is the required triangle Proof Based on G is the gravity center Diagram Go to Begin GE 27 03. Circle : Three corcles touch each other with common tangent Diagram Question Three circles as shown in Figure 103 Circle A has radius a Circle B has radius b Circle C has radius c Find the length of common tangent RT in terms of a and b Find the radius c interms of a and b Solution In right triangle ABD AB = a + b AD = a - b By Pythagorean law, we have BD^2 = AB^2 - AD^2 Hence BD^2 = (a + b)^2 - (a + b)^2 = 4*a*b Hence RT = BD = 2*Sqr(a*b) Find radius c of circle C Common tangent of circle A and C is RS = 2*Sqr(a*c) Common tangent of circle B and C is ST = 2*Sqr(b*c) Since RT = RS + ST Hence 2*Sqr(a*b) = 2*Sqr(a*c) + 2*Sqr(b*c) Simplified we have Sqr(c) = Sqr(a*b)/(Sqr(a) + Sqr(b)) Hence c = (a*b)/(a + b + 2*Sqr(a*b)) Go to Begin GE 27 04. Square with 4 semi-circle Diagram Question Square with side = a Use center of each side draw semi-circles with radius = a/2 Find the shaded area as shown in Figure 104 Solution The common area of the four semi-circles is 4*(area of semi-circle) - area of square Hence common area = 4*((pi*r^2)/2) - a^2 = 2*pi*(a^2/4) - a^2 = (pi/2 - 1)*a^2 Go to Begin GE 27 05. Circle inscribed an equilateral triangle Diagram Question As shown in Figure 105, find the area of the smallest circle Solution Let side of equilateral tiangle be a Height of equilateral triangle ABC is h = Sqr(3)*a/2 Hence large circle radius is r1 = h/3 The 2nd large circle radius is r2 = r1/3 = (h/3)/3 = h/(3^2) The 3rd large circle radius is r3 = r2/3 = h/(3^3) Hence r3 = (0.5*Sqr(3)*a)/27 Hence area of small circle = pi*(r3)^2 Go to Begin GE 27 06. Circle inscribed an equilateral triangle Diagram Question 1. Find the total area of the small circles as shown in Figure 106 2. Find the ratio of area of triangle and the total area of circles Solution of question 1 Let side of equilateral tiangle be a Height of equilateral triangle ABC is h = Sqr(3)*a/2 Hence large circle radius is r1 = h/3 The 2nd large circle radius is r2 = r1/3 = (h/3)/3 = h/(3^2) Hence area of 3 small circle is Area = 3*pi*(r2)^2 Area = 3*pi*(h/9)^2 Area = 3*pi*(1.5*Sqr(3)/9)^2 Solution of question 2 Area of triangle = a*(a*Sqr(3)/2)/2 = (Sqr(3)*a^2)/4 Area of circles = pi*(r1)^2 + 3*pi*(r2)^2 r1 = h/3 = Sqr(3)*a/6 r2 = h/9 = Sqr(3)*a/18 Hence ratio = ? Go to Begin GE 27 07. Square inscribed an equilateral triangle Diagram Question As shown Figure 107 find ratio of area of equilateral triangle to square Solution Let side of square be a Triangle PQC is also equilateral triangle Hence height CE = Sqr(3)*a/2 Hence height CD = CE + ED = a*(1 + Sqr(3)/2) AB = AS + SR + RB = 2*AS + a Since triangle ASP similar to PEC, hence AS/PE = PS/CE Hence AS = PS*PE/CE = a/Sqr(3) Hence AB = 2*a/Sqr(3) + a = a*(1 + 2/Sqr(3)) Hence area of triangle ABC = AB*CD/2 = (a^2)*(1 + Sqr(3)/2)*(1 + 2/Sqr(3))/2 = (a^2)*(1 +7*Sqr(3)/12) Ratio of ABC : PQRS = (1 + 7*Sqr(3)/12) : 1 Go to Begin GE 27 08. Triangle : Area of triangle formed by medians Diagram Question As shown Figure 108, AD, BE and CF are medians of triangle ABC Use AD, BE, CF making a triangle PQR Find ratio of area triangle PQR to area of triangle ABC Solution : Use AHBG is parallelogram (Properties of medians of ABC) Let AG = 2*AD/3, AH = 2*BE/3 and GH = 2*CF/3 Construct triangle AGH Area of triangle AGH Let height of triangle ABC from C is h Height of triangle AFG is h/3 Height of triangle AHF is also h/3 Area of triangle AGH = area AGF + area AHF = (AB/2)*(h/3)/2 + (AB/2)*(h/3)/2 = (AB*h)/6 = (area of triangle ABC)/3 Triangle AGH and triangle PQR are similar (height of PQR)/(height of AGH) = 3/2 (area of PQR)/(area of AGH) = (3/2)^2 Hence area PQR = (9/4)*(area 0f AGH) = (9/4)*((area of triangle ABC)/3) = (3/4)*(area of triangle ABC) Hence (area of PQR) : (area of ABC) = 3 : 4 Go to Begin GE 27 09. Equilateral triangle : Medians and heights Diagram Question 1 Median and height of equilateral triangle coincide Proof Draw CF perpendicular to AB. Hence CF is the height Since CA = CB Hence CF bisects side AB and F is the mid-point of side AB Hence CF is also the median Question 2 : In equilateral triangle The in-center, circum center, gravity center and ortho-center coincide Proof Three heights meet at O and it is the orthocenter Three medians meet at O and it is the graivty center CF is also the bisector of angle ACB Since triangle CAF is congruent to triangle CBF Hence angle AFC = angle BFC Hence CF is the bisector of angle ACB Similarly, AD and BE are also angle bisectors Hence O is the in-center OF is bisector of side AB Since OF perpendicualr to AB and AF = FB Hence OF is bisector of side AB Similarly, OD is bisector BC and OE is bisector of CA Hence O is the circum-center Question Find area of pedal triangle of equilateral triangle ABC Solution Triangle DEF is the pedal triangle D and E are mid-points and DE = AB/2 Similarly EF =BC/2 and FD = CA/2 Hence Petal triangle DEF is equilateral Hence area of pedal triangle DEF is area ABC/4 Go to Begin GE 27 10. Pedal triangle of equilateral triangle Diagram Question Find area of pedal triangle of equilateral triangle ABC Solution Triangle DEF is the pedal triangle D and E are mid-points and DE = AB/2 Similarly EF =BC/2 and FD = CA/2 Hence Petal triangle DEF is equilateral Hence area of pedal triangle DEF is area ABC/4 Go to Begin GE 27 11. Ex-central triangle of equilateral triangle Diagram Question Find area of ex-central triangle of equilateral triangle ABC Solution Ex-centers Bisector of angle A and bisectors of two external angle meet at J It is the ex-center. Similarly, K and L are also ex-center J, C, K are colinear Angle JCB = (Ex-ternal angle C)/2 Angle BCO = (angle C)/2 Hence angle JCO is 90 degrees Similarly, angle KCO is 90 degrees Hence J, C, K are colinear K, A, L are also colinear L, B, J are also colinear Hence JKL make triangle with A, B, C on their sides Triangle JKL is call ex-central triangle Area of JCB = Area ABC Since JCB = JBC = 60 degrees Hence triangle JBC is equilateral triangle Similarly, KAC and LAB are equilateral triangle Hence area of JKL = 4*(area ABC) Go to Begin GE 27 12. Pedal triangle Diagram Study outlines 1. What is pedal triangle ? 2. AD is the bisector of angle EDF 3. Ortho-center of triangle ABC is the in-center of triangle DEF 4. Triangle ABC is the ex-central triangle of triangle DEF Text Pedal Triangle Text Go to Begin GE 27 13. Ex-central triangle Diagram Study outlines 1. What is ex-central triangle ? 2. Center of circle J is ex-circle between line AB and AC 3. J, C, K are colinear JC is bisector of external aangle of angle ACB LC is bisector of angle ACB Hence angle LCJ is 90 degrees Similarly, angle LCK is 90 degrees Hence J, C, K are colinear 4. CL perpendicular to JK 5. In-center of triangle ABC is also ortho-center of triangle JKL 6. Triangle ABC is the pedal triangle of triangle JKL 7. Radius of ex-circle Radius of circle J is s*tan(A/2) Radius of circle K is s*tan(B/2) Radius of circle L is s*tan(C/2) Where s = (AB + BC + CA)/2 Text Ex-central Triangle Text Go to Begin GE 27 14. Triangle : Divide into 4 congruent triangles Diagram Method Draw triangle ABC and find mid points D, E, F Join D, E, F then we have 4 congruent trangle Geometric proof Prove that triangle DEF is congruent to triangle AEF DE = AF and DE parallel to AB (Mid point rule) DF = AE and EF parallel to AC (Mid point rule) EF is common side of triangles DEF and AEF Hence triangle DEF is congruent to triangle AEF (SSS) Prove that triangle DEF is congruent to triangle CDE Same as above Prove that triangle DEF is congruent to triangle BDF Same as above Hence triangles DEF, AEF, BDF and CDE are congruent Go to Begin GE 27 15. Ortho-center, centroid and circum-center of triangle are colinear Diagram Geometric proof Geometry GE 16 12 Analytic geometric proof Analytic geometry AN 11 12 Go to Begin GE 27 16. Prove cos(A-B) = cos(A)*cos(B) + sin(A)*sin(B) Diagram Proof using cosine law fig01 Q02 Geometric method See trigonometry : TR 07 04 Go to Begin GE 27 17. 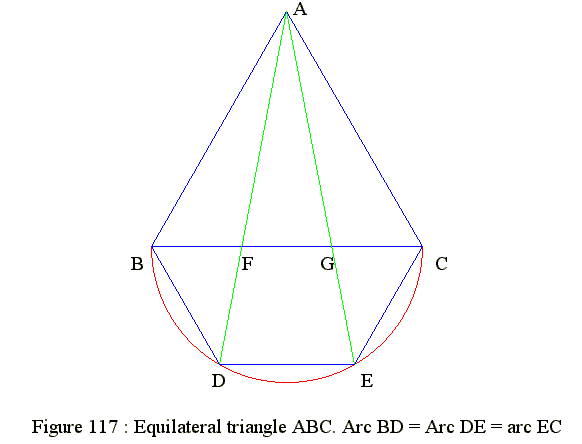Equilateral triangle : Divide side into 3 equal parts Diagram Method and proof fig01 Q03 Go to Begin GE 27 18. 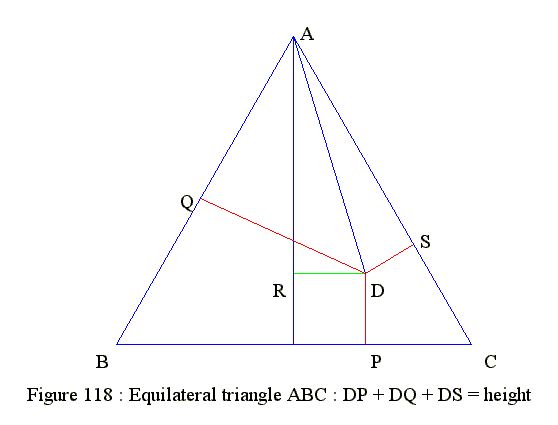Euilateral triangle : Sum of inside point to sides equals height Diagram Analytic geometric proof Give 3 points to make equilateral triangle ABC Give a point inside triangle D Distance to sides : DP, DQ and DS DP + DQ + DS = Heights Prove by computation or by construction Trigonometric method Triangle ADS : DS = AD*sin(DAS) Triangle ADQ : DQ = AD*sin(DAQ) Angle DAQ = 60 - angle DAS AR = AD*sin(30 - angle DAS) DS + DQ = AD*(sin(DAS) + sin(60 - DAS)) = AD*2*sin(60/2)*sin(30 - DAS) = AD*sin(30 - DAS) = AR Hence Height = DP + DQ + DS Go to Begin GE 27 19. Three points with one point varying Diagram Distance AC^2 = (7 - 0)^2 + (4 - k)^2 BC^2 = (3 - 0)^2 + (1 - k)^2 Find k if AC + BC = Minimum S = AC + BC = Sqr(49 + (4 - k)^2) + Sqr(9 + (1 - k)^2) Find minimum : dS/dk = 0 Find k if AC^2 + BC^2 = Minimum S = AC^2 + BC^2 = (49 + (4 - k)^2) + (9 + (1 - k)^2) Find minimum : dS/dk = 0 Go to Begin GE 27 20. Equilateral triangle : regular hexagon inscribed triangle Diagram Question Find the ratio of area triangle to area of hexagon Solution The side of regular hexagon is 1/3 of side triangle The regular hexagon can make 6 congruent equilateral triangles Hence are of hexagon = 6*(area of triangle) Hence are of triangle ABC = 9*(are of triangle) Hence the ratio is 9 : 6 Go to Begin GE 27 21. Heights of triangle ABC are concurrent Diagram Proof Geometry GE 03 03 : Ortho-center rule Q02 Go to Begin

---

Show Room of MD2002

Contact Dr. Shih

Math Examples Room

---

Copyright © Dr. K. G. Shih, Nova Scotia, Canada.

---